
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
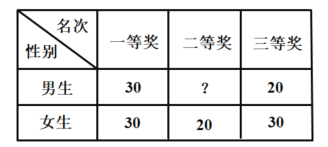
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
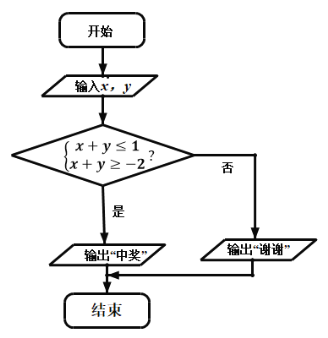
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
【答案】(1)30;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先设季军队的男运动员人数为n,由分层抽样的方法得关于n的等式,即可解得n;
(2)设男生为A1,A2,女生为B1,B2,B3,随机抽取3人,利用列举法写出所有基本事件和只有一个男生上台领奖基本事件,最后利用概率公式即可计算得解;
(3)由框图得到,点(x,y)满足条件 ,其表示的区域是图中阴影部分,利用几何概型的计算公式即可得到代表队队员获得奖品的概率.
,其表示的区域是图中阴影部分,利用几何概型的计算公式即可得到代表队队员获得奖品的概率.
(1)设代表队共有n人,则![]() ,
,
所以n=160,则三等奖代表队的男生人数为160![]() (30+30+20+20+30)=30,
(30+30+20+20+30)=30,
故所求二等奖代表队的男生人数为30人.
(2)设男生为A1,A2,女生为B1,B2,B3,随机抽取3人,包括的基本事件为A1A2B1,A1A2B2,A1A2B3,A1B1B2,
A1B1B3,A1B2B3,A2B1B2,A2B1B3,A2B2B3,B1B2B3,个数为10个,
只有一个男生上台领奖基本事件为A1B1B2,A1B1B3,A1B2B3,A2B1B2,A2B1B3,A2B2B3,个数为6个,
所以只有一个男生上台领奖的概率为![]() .
.
(3)试验的全部结果所构成的区域为Ω=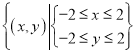 ,
,
面积为SΩ=4×4=16,
事件A表示代表队队员获得奖品,所构成的区域为A=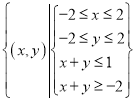 ,
,
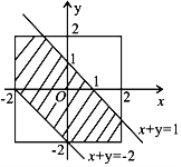
如图阴影部分的面积为:SA=4![]() ,
,
这是一个几何概型,所以P(A)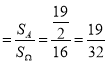 .
.
即代表队队员获得奖品的概率为![]() .
.
【点晴】
本小题主要考查古典概型及其概率计算公式、程序框图、几何概型等基础知识,考查运算求解能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
. ![]() 为椭圆的右焦点,
为椭圆的右焦点, ![]() 为椭圆上关于原点对称的两点,连接
为椭圆上关于原点对称的两点,连接![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
⑴求椭圆的标准方程;
⑵若![]() ,求
,求![]() 的值;
的值;
⑶设直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面凸六边形![]() 的边长相等,其中
的边长相等,其中![]() 为矩形,
为矩形,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折至
折至![]() ,
,![]() ,且均在同侧与平面
,且均在同侧与平面![]() 垂直,连接
垂直,连接![]() ,如图所示,E,G分别是
,如图所示,E,G分别是![]() ,
,![]() 的中点.
的中点.
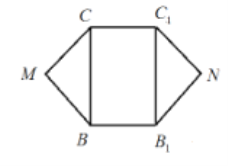
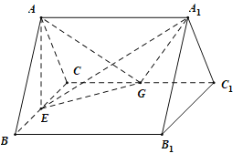
(1)求证:多面体![]() 为直三棱柱;
为直三棱柱;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正项数列![]() 的首项为
的首项为![]() ,且当数列
,且当数列![]() 是公比为
是公比为![]() 的等比数列时,则称数列
的等比数列时,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:数列
,证明:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若数列![]() 为“
为“![]() 数列”,且对任意
数列”,且对任意![]() ,
,![]() 、
、![]() 、
、![]() 成等差数列,公差为
成等差数列,公差为![]() .
.
①求![]() 与
与![]() 间的关系;
间的关系;
②若数列![]() 为递增数列,求
为递增数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
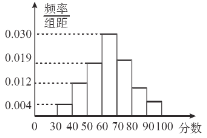
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该地区小学的这些学生中随机抽取3人,记这3人中成绩位于区间![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com