
【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1、2、3、4、5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
f | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件;求a、b、c的值.
(2)在(1)的条件下,将等级系数为4的3件记为x1、x2、x3,等级系数为5的2件记为y1、y2.现从这五件日用品中任取2件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某自动包装机包袋的食盐中,随机抽取![]() 袋作为样本,按各袋的质量(单位:
袋作为样本,按各袋的质量(单位: ![]() )分成四组,
)分成四组, ![]() ,相应的样本频率分布直方图如图所示.
,相应的样本频率分布直方图如图所示.
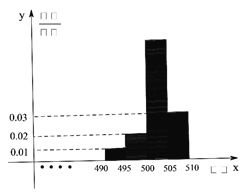
(Ⅰ)估计样本的中位数是多少?落入![]() 的频数是多少?
的频数是多少?
(Ⅱ)现从这台自动包装机包袋的大批量食盐中,随机抽取![]() 袋,记
袋,记![]() 表示食盐质量属于
表示食盐质量属于![]() 的袋数,依样本估计总体的统计思想,求
的袋数,依样本估计总体的统计思想,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题:
①![]() 在定义域上单调递增;
在定义域上单调递增;
②若锐角![]() ,
,![]() 满足
满足![]() ,则
,则![]() ;
;
③![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() ;
;
④函数![]() 的一个对称中心是
的一个对称中心是![]() ;
;
其中真命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数是食品支出总额占个人消费支出总额的比重.恩格尔系数越小,即家庭的消费支出中用于购买食物的支出所占比例越小,更多的消费用于精神追求,标志着家庭越富裕.恩格尔系数达59%以上为贫困,50~59%为温饱,40~50%为小康,30~40%为富裕,低于30%为最富裕.下图给出了1980—2017年我国城镇居民和农村居民家庭恩格尔系数的变化统计图,对所列年份进行分析,则下列结论正确的是( )

A.农村和城镇居民家庭消费支出呈下降趋势
B.农村居民家庭比城镇居民家庭用于购买食品的支出更多
C.1995年我国农村居民初步达到小康标准
D.2015年城镇和农村居民食品支出占个人消费支出总额之比大于30.6%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有区间
有区间![]() 上有一个零点,求实数
上有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com