
如图,四棱锥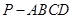 的底面是正方形,
的底面是正方形,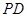 ⊥底面
⊥底面 ,点
,点 在棱
在棱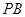 上.
上.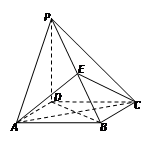
(1)求证:平面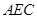 ⊥平面
⊥平面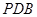 ;
;
(2)当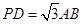 且
且 为
为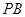 的中点时,求
的中点时,求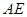 与平面
与平面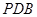 所成角的正弦值.
所成角的正弦值.
(Ⅰ)利用线面垂直证明面面垂直;(Ⅱ) 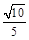 .
.
解析试题分析:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,∴PD⊥AC,∴AC⊥平面PDB,
又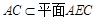 ,∴平面AEC⊥平面PDB. (6分)
,∴平面AEC⊥平面PDB. (6分)
(Ⅱ)方法一:如图1,设AC∩BD=O,连接OE, 
由(Ⅰ)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所成的角,
∵O,E分别为DB、PB的中点,∴OE∥PD,且OE= PD,
PD,
又∵PD⊥底面ABCD, ∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,由PD= AB,
AB,
设 ,则
,则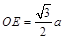 ,
, ,∴
,∴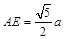 ,于是
,于是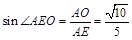 ,
,
即AE与平面PDB所成角的正弦值为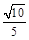 . (12分)
. (12分)
方法二:如图2,以D为原点建立空间直角坐标系D?xyz,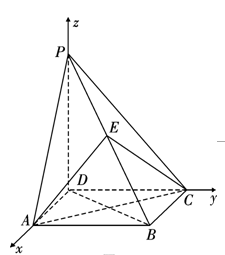
设 ,AE与平面PDB所成的角为
,AE与平面PDB所成的角为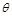 ,
,
则 ,
, ,
, ,
, ,
,
于是 ,所以
,所以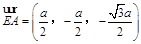 ,
,
且平面 的法向量
的法向量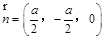 ,所以
,所以 ,
,
即AE与平面PDB所成角的正弦值为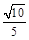 . (12分)
. (12分)
考点:本题考查了空间中的线面关系及空间角的求法
点评:直线和平面成角的重点是研究斜线和平面成角,常规求解是采用“作、证、算”,但角不易作出时,可利用构成三条线段的本质特征求解,即分别求斜线段、射影线段、点A到平面的距离求之.


科目:高中数学 来源: 题型:解答题
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.

(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图梯形ABCD,AD∥BC,∠A=900,过点C作CE∥AB,AD=2BC,AB=BC,,现将梯形沿CE
折成直二面角D-EC-AB.
(1)求直线BD与平面ABCE所成角的正切值;
(2)设线段AB的中点为 ,在直线DE上是否存在一点
,在直线DE上是否存在一点 ,使得
,使得 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB, PC的中点 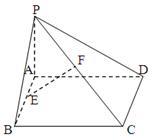
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与平面ABCD所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
(Ⅰ)求证:BF AD;
AD;
(Ⅱ)求直线BD与平面BCF所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直角梯形ABCD中,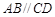 ,
,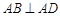 ,且
,且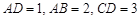 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且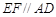 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
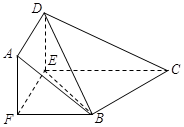
(Ⅰ)求证: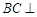 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com