
【题目】已知数列![]() ,
,![]() 满足:对于任意正整数n,当n≥2时,
满足:对于任意正整数n,当n≥2时,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,且数列
,且数列![]() 的各项均为正数.
的各项均为正数.
① 求数列![]() 的通项公式;
的通项公式;
② 是否存在![]() ,且
,且![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)84;(2)①![]() (
(![]() );②
);②![]() ,理由见解析.
,理由见解析.
【解析】
(1)在已知数列递推公式分别取![]() 为
为![]() ,累加可得
,累加可得![]() 的值;
的值;
(2)① 利用累加法求得![]() ,开方后求得数列
,开方后求得数列![]() 的通项公式;
的通项公式;
②由数列的通项公式求出![]() ,设
,设![]() ,得到
,得到![]() ,列出不等式组,即可求解.
,列出不等式组,即可求解.
(1)由题意,因为![]() ,且
,且![]() ,
,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,各式相加,可得
,各式相加,可得![]() .
.
(2)由![]() ,且
,且![]() ,
,
可得![]() ,
,![]() ,
,![]() ,…,
,…,![]() .
.
将上面的式子相加,得![]() ,
,
所以![]() .
.
因为{an}的各项均为正数,故![]()
![]() .
.
因为![]() 也适合上式,所以
也适合上式,所以![]() (
(![]() ).
).
② 假设存在满足条件的k ,不妨设![]() ,
,
所以![]() , 平方得
, 平方得![]() ,(*)
,(*)
所以![]() ,
,
所以![]() 且
且![]() ,即
,即![]()
由(1)得,![]() ,即
,即![]() ,
,
若![]() ,代入(*)式,求得
,代入(*)式,求得![]() 不合,舍去;
不合,舍去;
若![]() ,结合(2)得
,结合(2)得![]() ,
,
所以![]() ,即
,即![]() ,又
,又![]() 且
且![]() ,
,
所以![]() 的可能取值为2,34,代入(*)式逐一计算,可求得
的可能取值为2,34,代入(*)式逐一计算,可求得![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为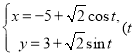 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
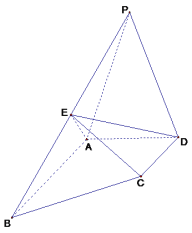
(1)求证:平面PAB⊥平面CDE;
(2)若AD=CD=2,求点P到平面ADE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x2+1,g(x)=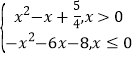 ,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
(1)证明数列![]() 为等差数列,并求出数列
为等差数列,并求出数列![]() 的通项公式.
的通项公式.
(2)若不等式![]() ,对任意
,对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)记数列 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,
,![]() 使得
使得![]() 成立,若存在,求出所有符合条件的有序实数对(
成立,若存在,求出所有符合条件的有序实数对(![]() ,
,![]() );若不存在,请说明理由.
);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.若“![]() ”为假命题,则“
”为假命题,则“![]() ”为假命题
”为假命题
B.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+1|>|2﹣x|+1的解集为M,且a,b,c∈M.
(1)比较|a﹣b|与|1﹣ab|的大小,并说明理由;
(2)若![]() ,求a2+b2+c2的最小值.
,求a2+b2+c2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com