【题目】定义在[0，1]上的函数f（x）满足：①f（0）=0；②f（x）+f（1﹣x）=1；③f（ 
）= 
f（x）；④当0≤x1＜x2≤1时，f（x1）≤f（x2）．则f（ 
）= ．
【答案】
【解析】解：∵函数f（x）在[0，1]上为非减函数，且①f（0）=0；③f（1﹣x）+f（x）=1， 令x=1可得f（1）=1．
∵f（ 
）= 
f（x）；
∴f（ 
）= f（1）= ；
再由③可得f（ ）+f（1﹣ ）=1，故有f（ 
）= ．
对于②f（ ）= f（x）；
由此可得 f（ 
）= f（ ）= 
，f（ 
）= f（ ）= 
、f（ 
）= f（ ）= 
、f（ 
）= 
．f（ 
）= 
，f（ 
）=
令x= ，由f（ ）= ，可得 f（ 
）= ，f（ 
）= ，f（ 
）= ，f（ 
）= ．f（ 
）= ，f（ 
）=
再 ＜ 
＜ ，可得 =f（ ）≤f（ ）≤f（ ）= ，
得f（ ）= ，
所以答案是
科目：高中数学 来源： 题型：
【题目】已知函数
， 
.
（Ⅰ）若曲线
在点
处的切线与直线
垂直，求函数
的极值；
（Ⅱ）设函数
.当
时，若区间
上存在
，使得
，求实数
的取值范围.（
为自然对数底数）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】由小到大排列的一组数据x1 ， x2 ， x3 ， x4 ， x5 ， 其中每个数据都小于﹣1，则样本1，x1 ， ﹣x2 ， x3 ， ﹣x4 ， x5的中位数为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a≥0，f（x）=x﹣1﹣ln2x+2alnx（x＞0）．
（1）令F（x）=xf′（x），讨论F（x）在（0，+∞）内的单调性并求极值；
（2）求证：当x＞1时，恒有x＞ln2x﹣2alnx+1．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB=AC，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．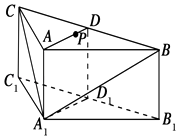 
（1）在平面ABC内，试作出过点P与平面A1BC平行的直线l，并说明理由；
（2）证明：直线l⊥平面ADD1A1 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
．
（1）当 
时，求函数f（x）的取值范围；
（2）将f（x）的图象向左平移 
个单位得到函数g（x）的图象，求g（x）的单调递增区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某媒体为调查喜爱娱乐节目
是否与观众性别有关，随机抽取了30名男性和30名女性观众，抽查结果用等高条形图表示如图：
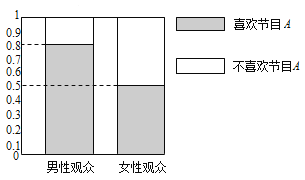
（1）根据该等高条形图，完成下列
列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
与观众性别有关？
（2）从性观众中按喜欢节目
与否，用分层抽样的方法抽取5名做进一步调查．从这5名中任选2名，求恰有1名喜欢节目
和1名不喜欢节目
的概率．
附：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
．
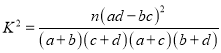查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
