Question

【题目】已知函数.

(1)求函数的最小值及取到最小值时自变量x的集合；

(2)指出函数y＝的图象可以由函数y＝sinx的图象经过哪些变换得到；

(3)当x∈[0，m]时，函数y＝f(x)的值域为，求实数m的取值范围．

Answer 1

【答案】(1) ，；(2)见解析；(3) .

【解析】

(1)利用正弦函数的性质求出最小值以及取到最小值时自变量x的集合；

(2)由正弦函数的相位变换、周期变换、振幅变换描述即可；

(3)画出函数的图像，根据图像找到值域为的图像，即可确定实数m的取值范围.

(1)，此时，即，

即此时自变量x的集合是.

(2)把函数y＝sinx的图象向右平移个单位长度，得到函数的图象，再把函数的图象上所有点的纵坐标不变，横坐标缩短为原来的，得到函数的图象，最后再把函数的图象上所有点的横坐标不变，纵坐标伸长为原来的2倍，得到函数的图象．

(3)如图，因为当x∈[0，m]时，y＝f(x)取到最大值2，所以.

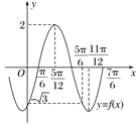
又函数y＝f(x)在上是减函数，

故m的最大值为内使函数值为的值，

令，得，所以m的取值范围是.