
【题目】如图,在直三棱柱![]() 中,
中,![]() 分别是棱
分别是棱![]() 上的点(点
上的点(点![]() 不同于点
不同于点![]() ),且
),且![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.

求证:(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)推导出BB1⊥AD,AD⊥DE,从而AD⊥平面BCC1B1,由此能证明平面ADE⊥平面BCC1B1.(2)推导出BB1⊥平面A1B1C1,BB1⊥A1F,A1F⊥B1C1,从而A1F⊥平面BCC1B1,再由AD⊥平面BCC1B1,得A1F∥AD,由此能证明A1F∥平面ADE.
(1)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,因为AD平面ABC,所以BB1⊥AD,
又因为AD⊥DE,在平面BCC1B1中,BB1与DE相交,
所以AD⊥平面BCC1B1,
又因为AD平面ADE,所以平面ADE⊥平面BCC1B1.
(2)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面A1B1C1,
因为A1F平面A1B1C1,所以BB1⊥A1F,
又因为A1F⊥B1C1,
在平面BCC1B1中,BB1∩B1C1=B1,
所以A1F⊥平面BCC1B1,
在(1)中已证得AD⊥平面BCC1B1,
所以A1F∥AD,又因为A1F平面ADE,AD![]() 平面ADE,
平面ADE,
所以A1F∥平面ADE.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中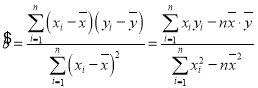 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左焦点为
的左焦点为![]() ,点A的坐标为(0,1),点P为双曲线右支上的动点,且△APF1周长的最小值为6,则双曲线的离心率为( )
,点A的坐标为(0,1),点P为双曲线右支上的动点,且△APF1周长的最小值为6,则双曲线的离心率为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
, ![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 内一点
内一点![]() 作两条相互垂直的弦
作两条相互垂直的弦![]() ,当
,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
(3)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点, ![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com