
科目:高中数学 来源:最新名师点评测试卷 高一数学 第一册上 题型:044
某林场原有森林木材存有量为 a,林木以每年25%的增长率生长,而每年冬天要砍伐的木材量为x,为实现经过20年达到木材存有量翻两番,求每年砍伐量x的最大值.
查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:044
某林场原有森林木材量a,木材以每年25%的增长率生成,而每年要砍伐的木材量为x,为使经过20年木材存有量翻两番,求每年砍伐量x.(取lg2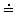 0.3)
0.3)
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源: 题型:044
某林场原有森林木材量为a,木材每年以25%的增长率生长,而每年砍伐的木材量为x,为使第20年末木材存有量翻两番,求每年砍伐量x.(取lg2=0.3).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com