
(本题满分15分)如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
 (Ⅰ)证明:
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() 为
为![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
满分15分。
(Ⅰ)证明:由四边形![]() 为菱形,
为菱形,![]() ,可得
,可得![]() 为正三角形.
为正三角形.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,因此
,因此![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() 且
且![]() ,
,
所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
所以![]() . …………………………………7分
. …………………………………7分
(Ⅱ)解:设![]() ,
,![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() .
.
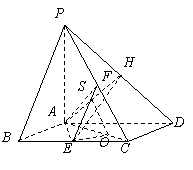 由(Ⅰ)知
由(Ⅰ)知![]() 平面
平面![]() ,
,
则![]() 为
为![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,
所以当![]() 最短时,
最短时,![]() 最大,
最大,
即当![]() 时,
时,![]() 最大.
最大.
此时![]() ,
,
因此![]() .又
.又![]() ,所以
,所以![]() ,
,
所以![]() . ………………………………………10分
. ………………………………………10分
解法一:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,
,
过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,
又![]() 是
是![]() 的中点,在
的中点,在![]() 中,
中,![]() ,
,
又![]() ,在
,在![]() 中,
中,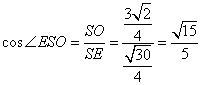 ,即所求二面角的余弦值为
,即所求二面角的余弦值为![]() .……………14分
.……………14分
解法二:
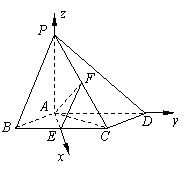 由(Ⅰ)知
由(Ⅰ)知![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又![]() 分别为
分别为![]() 的中点,所以
的中点,所以
![]() ,
,
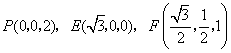 ,
,
所以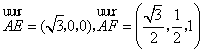 .
.
设平面![]() 的一法向量为
的一法向量为![]() ,
,
则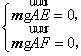 因此
因此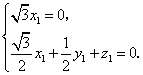
取![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() 为平面
为平面![]() 的一法向量.
的一法向量.
又![]() ,所以
,所以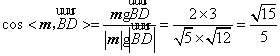 .
.
因为二面角![]() 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为![]() .………………14分
.………………14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
|
设![]() 的夹角为
的夹角为![]()
的取值范围; (III)设以点N(0,m)为圆心,以![]() 为
为
半径的圆与曲线E在第一象限的交点H,若圆在点H处的
切线与曲线E在点H处的切线互相垂直,求实数m的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州八校高三9月期初联考文科数学试卷(解析版) 题型:解答题
(本题满分15分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, 与平面
与平面 所成角的正切值依次是
所成角的正切值依次是 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷三 题型:解答题
(本题满分15分)如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF= 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF.
(I)求二面角 的余弦值;
的余弦值;
(II)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使C
与 重合,求线段FM的长.
重合,求线段FM的长.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三年级随堂练习数学试卷 题型:解答题
(本题满分15分)
如图:某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
.
(Ⅰ)试将污水净化管道的长度 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)问:当 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.

查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(浙江卷)理科数学 题型:解答题
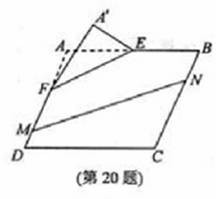 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别
在线段 上,
上, .沿直线
.沿直线
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四
边形 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段
的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com