
【题目】某种病毒感染性腹泻在全世界范围内均有流行,感染对象主要是成人和学龄儿童,寒冷季节呈现高发,据资料统计,某市11月1日开始出现该病毒感染者,11月1日该市的病毒新感染者共有20人,此后每天的新感染者比前一天的新感染者增加50人,由于该市医疗部分采取措施,使该病毒的传播速度得到控制,从第![]() 天起,每天的新感染者比前一天的新感染者减少30人,直到11月30日为止.
天起,每天的新感染者比前一天的新感染者减少30人,直到11月30日为止.
(1)设11月![]() 日当天新感染人数为
日当天新感染人数为![]() ,求
,求![]() 的通项公式(用
的通项公式(用![]() 表示);
表示);
(2)若到11月30日止,该市在这30日感染该病毒的患者共有8670人,11月几日,该市感染此病毒的新患者人数最多?并求出这一天的新患者人数.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)11月12日,该市感染此病毒的新患者人数最多,这一天的新患者人数为570人.
;(2)11月12日,该市感染此病毒的新患者人数最多,这一天的新患者人数为570人.
【解析】
(1)分析可得当![]() 时为公差是50的等差数列,当
时为公差是50的等差数列,当![]() 时为公差是
时为公差是![]() 的等差数列.分段求出对应的通项公式即可.
的等差数列.分段求出对应的通项公式即可.
(2)由(1)中的通项公式知患者人数先增再减,算出分段处即第![]() 天的患者人数即为最大值.
天的患者人数即为最大值.
(1)由题意得, 当![]() 时是以公差为50,首项为20的等差数列,
时是以公差为50,首项为20的等差数列,
此时![]() ,(
,(![]() ).
).
当![]() 时是以公差是
时是以公差是![]() ,首项为
,首项为![]() 的等差数列,
的等差数列,
此时![]()
故![]() ,
,![]() ,
,![]() .
.
(2)由(1)可知,前![]() 日患者共有
日患者共有![]() 人.
人.
又第![]() 日有
日有![]() 人,
人,
第30日有![]() 人.故
人.故![]() 日至30日共
日至30日共![]() 天的时间里共有
天的时间里共有
![]() 人
人
故1到30日共有![]() 人
人
故![]() 即
即![]() ,又
,又![]()
故![]() .当天新增患病人数为
.当天新增患病人数为![]() 人.
人.
故11月12日,该市感染此病毒的新患者人数最多,这一天的新患者人数为570人


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
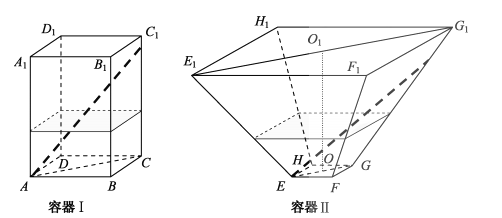
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2019年1月1日 | 4000 | 0.125 | 280 |
2019年1月2日 | 4100 | 0.126 | 146 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=![]() ,剩余续航里程=
,剩余续航里程=![]() ,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于12.5B. 12.5到12.6之间
C. 等于12.6D. 大于12.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() 为
为![]() 上的奇函数,则称
上的奇函数,则称![]() 是位差值为
是位差值为![]() 的“位差奇函数”.
的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否为位差奇函数?说明理由;
是否为位差奇函数?说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若![]() 对任意属于区间
对任意属于区间![]() 中的
中的![]() 都不是位差奇函数,求实数
都不是位差奇函数,求实数![]() 、
、![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,其图象上任一点
,其图象上任一点![]() 都满足
都满足![]() .
.
①函数![]() 一定是偶函数;②函数
一定是偶函数;②函数![]() 可能既不是偶函数也不是奇函数;
可能既不是偶函数也不是奇函数;
③函数![]() 若是偶函数,则值域是
若是偶函数,则值域是![]() 或
或![]() ;④函数
;④函数![]() 可以是奇函数;
可以是奇函数;
⑤函数![]() 的值域是
的值域是![]() ,则
,则![]() 一定是奇函数.
一定是奇函数.
其中正确命题的序号是__________(填上所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)令![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令![]() ,
,![]() 的最大值为A,函数
的最大值为A,函数![]() 在区间
在区间![]() 上单调递增函数,求
上单调递增函数,求![]() 的取值范围;
的取值范围;
(3)令![]() ,将函数
,将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图像,对任意
的图像,对任意![]() ,求
,求![]() 在区间
在区间![]() 上零点个数的所有可能值.
上零点个数的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com