
【题目】学校书店新进了一套精品古典四大名著:《红楼梦》、《三国演义》、《西游记》、《水浒传》共四本书,每本名著数量足够多,今有五名同学去书店买书,由于价格较高,五名同学打算每人只选择一本购买.
(1)求“每本书都有同学买到”的概率;
(2)求“对于每个同学,均存在另一个同学与其购买的书相同”的概率;
(3)记X为五位同学购买相同书的个数的最大值,求X的分布列和数学期望E(X).
【答案】(1)![]() ,(2)
,(2)![]() ,(3)分布列见解析,
,(3)分布列见解析,![]()
【解析】
(1)等价于“两名同学买同一种书,3名同学买3种不同的书”,再根据古典概型的概率公式可得结果;
(2)包含两种情况:①五名同学买同一种书,②两名同学买同一种书,另外三名同学买同一种书,再根据古典概型的概率公式可得结果;
(3)![]() 的所有可能取值为:5,4,3,2,根据古典概型的概率公式可得
的所有可能取值为:5,4,3,2,根据古典概型的概率公式可得![]() 的各个取值的概率,由此可得分布列,根据期望公式可得期望.
的各个取值的概率,由此可得分布列,根据期望公式可得期望.
(1)“每本书都有同学买到”等价于“两名同学买同一种书,3名同学买3种不同的书”
所以所求事件的概率为:![]()
![]() ,
,
(2)“对于每个同学,均存在另一个同学与其购买的书相同”包含两种情况:①五名同学买同一种书,②两名同学买同一种书,另外三名同学买同一种书,
因此所求概率为![]()
![]() ,
,
(3)![]() 的所有可能取值为:5,4,3,2,
的所有可能取值为:5,4,3,2,
则![]() ,
,
![]() ,
,
![]() ,
,
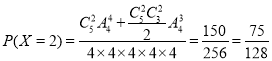 ,
,
所以![]() 的分布列为:
的分布列为:
| 5 | 4 | 3 | 2 |
|
|
|
|
|
所以![]()
![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】某鲜奶店每天购进30瓶鲜牛奶,且当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式![]() (n∈N).鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶)绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5):
(n∈N).鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶)绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5):
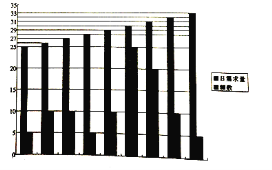
(1)求这100天的日利润(单位:元)的平均数;
(2)以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上,O为坐标原点.
在椭圆C上,O为坐标原点.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设动直线l与椭圆C有且仅有一个公共点,且l与圆
设动直线l与椭圆C有且仅有一个公共点,且l与圆![]() 的相交于不在坐标轴上的两点
的相交于不在坐标轴上的两点![]() ,
,![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 |
产品销量y(件) | q | 85 | 82 | 80 | 75 |
已知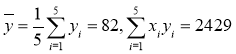
(1)求出q的值;
(2)已知变量![]() 具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程
具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(3)假设试销单价为10元,试估计该产品的销量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]()
(1)若“![]() x∈A,使得x∈B”为真命题,求m的取值范围;
x∈A,使得x∈B”为真命题,求m的取值范围;
(2)是否存在实数m,使“x∈A”是“X∈B”必要不充分条件,若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=23x.
(1)证明:f(x)-g(x)=23-x,并求函数f(x),g(x)的解析式;
(2)解关于x不等式:g(x2+2x)+g(x-4)>0;
(3)若对任意x∈R,不等式f(2x)≥mf(x)-4恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查统计,网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 三种商品有购买意向.该淘宝小店推出买一种送5元优惠券的活动.已知某网民购买
三种商品有购买意向.该淘宝小店推出买一种送5元优惠券的活动.已知某网民购买![]() 商品的概率分别为
商品的概率分别为![]() ,
,![]() ,
,![]() ,至少购买一种的概率为
,至少购买一种的概率为![]() ,最多购买两种的概率为
,最多购买两种的概率为![]() .假设该网民是否购买这三种商品相互独立.
.假设该网民是否购买这三种商品相互独立.
(1)求该网民分别购买![]() 两种商品的概率;
两种商品的概率;
(2)用随机变量![]() 表示该网民购买商品所享受的优惠券钱数,求
表示该网民购买商品所享受的优惠券钱数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
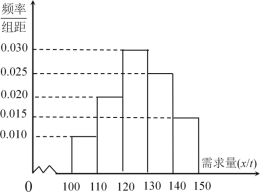
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的安全意识,某中学举行了一次“安全自救”的知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
序号(i) | 分组(分数) | 组中值(Gi) | 频数(人数) | 频率(fi) |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1.00 | ||
(1)求出频率分布表中①②③④⑤处的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生能获奖;
(3)求这800名学生的平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com