
(07年湖北卷理)(12分)
如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]()
![]() .
.
(I)求证:平面![]()
![]() ;
;
(II)当角![]() 变化时,求直线
变化时,求直线![]() 与平面
与平面![]() 所成的角的取值范围.
所成的角的取值范围.

本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力.
解析:解法1:(Ⅰ)![]() ,
,![]() 是等腰三角形,又
是等腰三角形,又![]() 是
是![]() 的中点,
的中点,
![]() ,又
,又![]() 底面
底面![]() .
.![]() .于是
.于是![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ) 过点![]() 在平面
在平面![]() 内作
内作![]() 于
于![]() ,则由(Ⅰ)知
,则由(Ⅰ)知![]() 平面
平面![]() .
.
连接![]() ,于是
,于是![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ;
;
设![]() ,在
,在![]() 中,
中,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .又
.又![]() ,
,![]() .
.
即直线![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.

解法2:(Ⅰ)以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
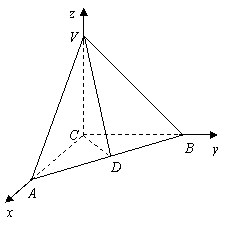
则 ,
,
于是, ,
,![]() ,
,![]() .
.
从而![]() ,即
,即![]() .
.
同理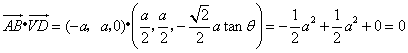 ,
,
即![]() .又
.又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() .
.
得
可取![]() ,又
,又![]() ,
,
于是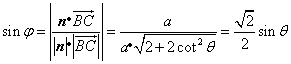 ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() .
.
即直线![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.
解法3:(Ⅰ)以点![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,

则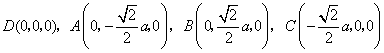 ,
,
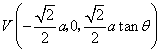 ,于是
,于是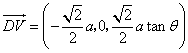 ,
,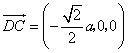 ,
,![]() .
.
从而![]()
 ,即
,即![]() .
.
同理 ,即
,即![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() ,得
,得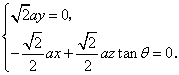
可取![]() ,又
,又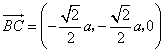 ,
,
于是 ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.
解法4:以![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
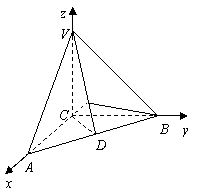
则![]() .
.
设![]() .
.
(Ⅰ)![]() ,
,
![]() ,
,
即![]() .
.
![]() ,
,
即![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
设![]() 是平面
是平面![]() 的一个非零法向量,
的一个非零法向量,
则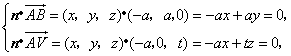 取
取![]() ,得
,得![]() .
.
可取![]() ,又
,又![]() ,
,
于是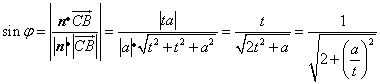 ,
,
![]() ,
,![]() 关于
关于![]() 递增.
递增.
![]() ,
,![]() .
.
即直线![]() 与平面
与平面![]() 所成角的取值范围为
所成角的取值范围为![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
(07年湖北卷理)(12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(I)在答题卡上完成频率分布表,并在给定的坐标系中画出频率分布直方图;
(II)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此,估计纤度的期望.
)作为代表.据此,估计纤度的期望.
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com