
已知函数![]() 其中
其中![]()
(1)证明函数f(x)的图像在y轴的一侧;
(2)求函数![]() 与
与![]() 的图像的公共点的坐标。
的图像的公共点的坐标。
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:2013-2014学年福建省福州市高三毕业班质检文科数学试卷(解析版) 题型:解答题
已知函数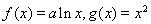 .其中
.其中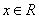 .
.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)-1对任意x>0恒成立,求实数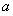 的值;
的值;
(3)当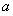 <0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为
<0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为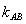 ,若
,若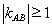 ,求
,求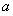 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏盐城第一中学高三第二学期期初检测文科数学试卷(解析版) 题型:解答题
已知函数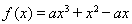 ,其中
,其中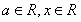 .
.
(1)当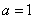 时,求函数
时,求函数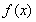 在
在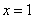 处的切线方程;
处的切线方程;
(2)若函数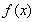 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围;
(3)已知 ,如果存在
,如果存在 ,使得函数
,使得函数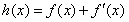
 在
在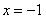 处取得最小值,试求
处取得最小值,试求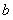 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2013届浙江宁波四校高二下学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
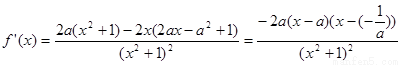 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当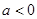 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 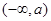 ,
,

 ,
, 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com