
【题目】如图所示,![]() 平面ABCD,
平面ABCD,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,M为AC的中点.
,M为AC的中点.
![]() 证明:
证明:![]() 平面PCD;
平面PCD;
![]() 若PD与平面PAC所成角的正切值为
若PD与平面PAC所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2)![]()
【解析】
![]() 因为M为等边
因为M为等边![]() 的AC边的中点,所以
的AC边的中点,所以![]() 依题意
依题意![]() ,且A、B、C、D四点共面,由此能证明
,且A、B、C、D四点共面,由此能证明![]() 平面PCD;
平面PCD;![]() 因为
因为![]() ,
,![]() ,所以
,所以![]() 平面PAC,故PD与平面PAC所成的角即为
平面PAC,故PD与平面PAC所成的角即为![]() ,在等腰
,在等腰![]() 中,过点M作
中,过点M作![]() 于点E,再在
于点E,再在![]() 中作
中作![]() 于点F,
于点F,![]() 即为二面角
即为二面角![]() 的平面角,由此能求出二面角
的平面角,由此能求出二面角![]() 的正切值.
的正切值.
![]() 证明:因为M为等边
证明:因为M为等边![]() 的AC边的中点,所以
的AC边的中点,所以![]() .
.
依题意![]() ,且A、B、C、D四点共面,所以
,且A、B、C、D四点共面,所以![]() .
.
又因为![]() 平面PCD,
平面PCD,![]() 平面PCD,所以
平面PCD,所以![]() 平面PCD.
平面PCD.
![]() 解:因为
解:因为![]() ,
,![]() ,
,
所以![]() 平面PAC,故PD与平面
平面PAC,故PD与平面
PAC所成的角即为![]() .
.
不妨设![]() ,则
,则![]() .
.
由于![]() ,所以
,所以![]() .
.
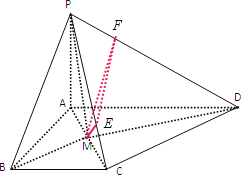
在等腰![]() 中,过点M作
中,过点M作![]() 于点E,
于点E,
再在![]() 中作
中作![]() 于点
于点![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 平面PCD,可得
平面PCD,可得![]() .
.
又![]() ,
,
所以![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
由题意知![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
即二面角![]() 的正切值是
的正切值是![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋里装有大小相同的5个小球,其中红色两个,其余3个颜色各不相同![]() 现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望
现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是______;若变量X为取出的三个小球中红球的个数,则X的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(已知:![]() 则认为
则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般,
线性相关性一般,![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y与x的线性回归方程,并预测该地区2019年足球特色学校的个数(精确到个位)
参考公式:
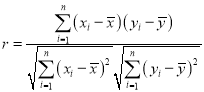
![]() ;
;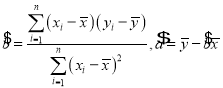
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如上图.现在图(3)中随机选取一个点,则此点取自阴影部分的概率为________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟.那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com