
【题目】直线![]() 与圆
与圆![]() 相交于两点
相交于两点![]() ,若
,若![]() ,
,![]() 为圆
为圆![]() 上任意一点,则
上任意一点,则![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
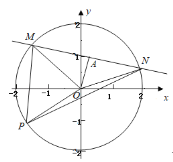
取MN的中点A,连接OA,则OA⊥MN.算出OA=1,得到∠AON,可得∠MON,计算出![]()
![]() 的值,运用向量的加减运算和向量数量积的定义,可得
的值,运用向量的加减运算和向量数量积的定义,可得![]() 2﹣4cos∠AOP,考虑
2﹣4cos∠AOP,考虑![]() ,
,![]() 同向和反向,可得最值,即可得到所求范围.
同向和反向,可得最值,即可得到所求范围.
取MN的中点A,连接OA,则OA⊥MN,
∵c2=a2+b2,
∴O点到直线MN的距离OA![]() 1,
1,
x2+y2=4的半径r=2,
∴Rt△AON中,设∠AON=θ,得cosθ![]() ,得θ=
,得θ=![]() ,
,
cos∠MON=cos2θ=![]() ,
,
由此可得,![]()
![]() |
|![]() ||
||![]() |cos∠MON
|cos∠MON
=2×2×(![]() )=﹣2,
)=﹣2,
则![]() (
(![]() )(
)(![]() )
)![]()
![]() 2
2![]() (
(![]() )
)
=﹣2+4﹣2![]()
![]() 2﹣2|
2﹣2|![]() ||
||![]() |cos∠AOP=2﹣4cos∠AOP,
|cos∠AOP=2﹣4cos∠AOP,
当![]() ,
,![]() 同向时,取得最小值且为2﹣4=﹣2,
同向时,取得最小值且为2﹣4=﹣2,
当![]() ,
,![]() 反向时,取得最大值且为2+4=6.
反向时,取得最大值且为2+4=6.
则![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比![]() .
.
(1)设圆![]() 求过
求过![]() (2,0)的直线关于圆
(2,0)的直线关于圆![]() 的距离比
的距离比![]() 的直线方程;
的直线方程;
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() (0,3)且直线
(0,3)且直线![]() =
= ![]() 关于圆
关于圆![]() 的距离比
的距离比![]() ,求此圆的
,求此圆的![]() 的方程;
的方程;
(3)是否存在点![]() ,使过
,使过![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
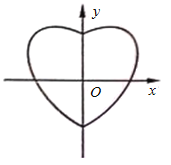
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在图1所示的梯形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,且
,且![]() .将梯形
.将梯形![]() 沿
沿![]() 对折,使平面
对折,使平面![]() 平面
平面![]() ,如图2所示,连接
,如图2所示,连接![]() ,取
,取![]() 的中点
的中点![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置,并给予证明;若不存在,请说明理由;
的位置,并给予证明;若不存在,请说明理由;
(3)设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com