
已知△ 的两个顶点
的两个顶点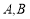 的坐标分别是
的坐标分别是 ,
,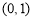 ,且
,且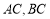 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(1)求顶点 的轨迹
的轨迹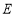 的方程,并判断轨迹
的方程,并判断轨迹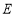 为何种圆锥曲线;
为何种圆锥曲线;
(2)当 时,过点
时,过点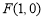 的直线
的直线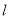 交曲线
交曲线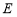 于
于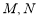 两点,设点
两点,设点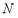 关于
关于 轴的对称点为
轴的对称点为 (
(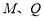 不重合), 试问:直线
不重合), 试问:直线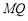 与
与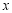 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
(1)详见解析;(2)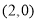 .
.
【解析】
试题分析:(1)设出顶点C的坐标,由AC,BC所在直线的斜率之积等于m(m≠0)列式整理得到顶点C的轨迹E的方程,然后分m的不同取值范围判断轨迹E为何种圆锥曲线;
(2)把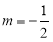 代入E得轨迹方程,由题意设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M,N两点的横坐标的和与积,由两点式写出直线MQ的方程,取y=0后求出x,结合根与系数关系可求得x=2,则得到直线MQ与x轴的交点是定点,并求出定点..
代入E得轨迹方程,由题意设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M,N两点的横坐标的和与积,由两点式写出直线MQ的方程,取y=0后求出x,结合根与系数关系可求得x=2,则得到直线MQ与x轴的交点是定点,并求出定点..
试题解析:(1)由题知: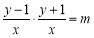
化简得: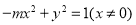 2分
2分
当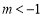 时 轨迹
时 轨迹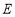 表示焦点在
表示焦点在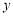 轴上的椭圆,且除去
轴上的椭圆,且除去 两点;
两点;
当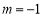 时 轨迹
时 轨迹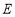 表示以
表示以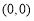 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去 两点;
两点;
当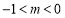 时 轨迹
时 轨迹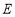 表示焦点在
表示焦点在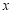 轴上的椭圆,且除去
轴上的椭圆,且除去 两点;
两点;
当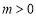 时 轨迹
时 轨迹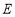 表示焦点在
表示焦点在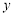 轴上的双曲线,且除去
轴上的双曲线,且除去 两点; 6分
两点; 6分
(2)设
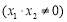
依题直线 的斜率存在且不为零,则可设
的斜率存在且不为零,则可设 :
: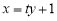 ,
,
代入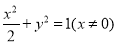 整理得
整理得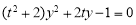
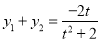 ,
,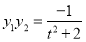 , 9分
, 9分
又因为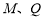 不重合,则
不重合,则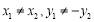
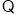
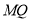 的方程为
的方程为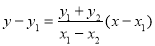 令
令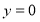 ,
,
得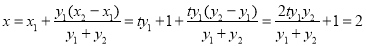
故直线 过定点
过定点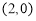 . 14分
. 14分
解二:设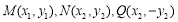
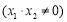
依题直线 的斜率存在且不为零,可设
的斜率存在且不为零,可设 :
: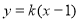
代入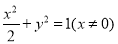 整理得:
整理得: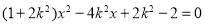
 ,
,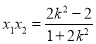 , 9分
, 9分
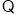
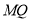 的方程为
的方程为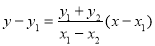 令
令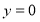 ,
,
得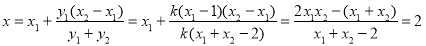
 直线
直线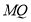 过定点
过定点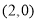 14分
14分
考点:1.椭圆的简单性质;2.与直线有关的动点轨迹方程.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源:2015届湖北部分重点中学高二上学期期末考试文科数学试卷(解析版) 题型:解答题
我们把离心率为e=的双曲线 (a>0,b>0)称为黄金双曲线.如图,
(a>0,b>0)称为黄金双曲线.如图,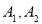 是双曲线的实轴顶点,
是双曲线的实轴顶点,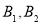 是虚轴的顶点,
是虚轴的顶点,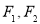 是左右焦点,
是左右焦点,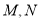 在双曲线上且过右焦点
在双曲线上且过右焦点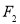 ,并且
,并且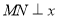 轴,给出以下几个说法:
轴,给出以下几个说法:

①双曲线x2-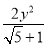 =1是黄金双曲线;
=1是黄金双曲线;
②若b2=ac,则该双曲线是黄金双曲线;
③如图,若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④如图,若∠MON=90°,则该双曲线是黄金双曲线.
其中正确的是( )
A.①②④ B.①②③ C.②③④ D.①②③④
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:填空题
多选题是标准化考试的一种题型,一般是从A、B、C、D四个选项中选出所有正确的答案.在一次考试中有5道多选题,某同学一道都不会,他随机的猜测,则他答对题数的期望值为 .
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:选择题
某运动会组委会要派五名志愿者从事翻译、导游、礼仪三项工作,要求每项工作至少有一人参加,则不同的派给方案共有
A.150种 B.180种 C.240种 D.360种
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测文数学试卷(解析版) 题型:填空题
设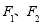 分别是双曲线C:
分别是双曲线C: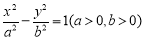 的左、右焦点,若双曲线右支上存在一点
的左、右焦点,若双曲线右支上存在一点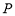 ,使
,使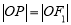 (
(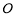 为原点),且
为原点),且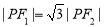 ,则双曲线的离心率为 .
,则双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测文数学试卷(解析版) 题型:选择题
在整数集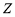 中,被
中,被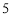 除所得余数为
除所得余数为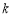 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为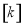 ,即
,即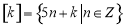 ,
,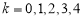 .给出如下四个结论:
.给出如下四个结论:
①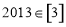 ;
;
②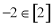 ;
;
③ ;
;
④当且仅当“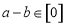 ”整数
”整数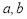 属于同一“类”.
属于同一“类”.
其中,正确结论的个数为.
A.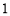 B.
B.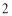 C.
C.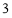 D.
D.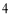
查看答案和解析>>
科目:高中数学 来源:2015届湖北孝感高级中学高二上学期期末考试理科数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知△ABC的顶点A(-6,0)和C(6,0),若顶点B在双曲线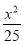 -
- =1的左支上,则
=1的左支上,则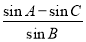 =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com