
【题目】如图所示,在四边形ABCD中,AB⊥DA,CE= ![]() ,∠ADC=
,∠ADC= ![]() ;E为AD边上一点,DE=1,EA=2,∠BEC=
;E为AD边上一点,DE=1,EA=2,∠BEC= ![]()
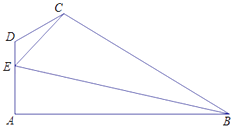
(1)求sin∠CED的值;
(2)求BE的长.
【答案】
(1)解:设∠CED=α.在△CED中,由余弦定理,得
CE2=CD2+DE2﹣2CD×DE×cos∠CDE,
得CD2+CD﹣6=0,解得CD=2(CD=﹣3舍去).
在△CED中,由正弦定理,得sin∠CED= ![]() .
.
(2)解:由题设知α∈(0, ![]() ),所以cos
),所以cos ![]() ,
,
而∠AEB= ![]() ,
,
所以cos∠AEB=cos( ![]() )
)
=cos ![]() cosα+sin
cosα+sin ![]() sinα
sinα
=﹣ ![]() cosα+
cosα+ ![]() sinα
sinα
=﹣ ![]()
= ![]() .
.
在Rt△EAB中,BE= ![]() =4
=4 ![]() .
.
【解析】(1)设∠CED=α.在△CED中,由余弦定理,可解得CD=2,在△CED中,由正弦定理可解得sin∠CED的值.(2)由题设知α∈(0, ![]() ),先求cos
),先求cos ![]() ,而∠AEB=
,而∠AEB= ![]() ,即可求cos∠AEB=cos(
,即可求cos∠AEB=cos( ![]() )的值.
)的值.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,其前n项和为Sn , 且满足a1=1,an+1=2 ![]() +1,n∈N* .
+1,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数k,使ak , S2k﹣1 , a4k成等比数列?若存在,求k的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin(2ωx+ ![]() )+
)+ ![]() +b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是
+b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是 ![]() ,最小值是
,最小值是 ![]() .
.
(1)求ω、a、b的值;
(2)求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,点![]() ,曲线
,曲线 ![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.
(1)在直角坐标系中,求点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com