
【题目】【2017山西三区八校二模】已知函数![]() (其中
(其中![]() ,
,![]() 为常数且
为常数且![]() )在
)在![]() 处取得极值.
处取得极值.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 在
在![]() 上的最大值为1,求
上的最大值为1,求![]() 的值.
的值.
【答案】(Ⅰ)单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由函数的解析式,可求出函数导函数的解析式,进而根据![]() 是
是![]() 的一个极值点
的一个极值点![]() ,可构造关于
,可构造关于![]() ,
,![]() 的方程,根据
的方程,根据![]() 求出
求出![]() 值;可得函数导函数的解析式,分析导函数值大于0和小于0时,
值;可得函数导函数的解析式,分析导函数值大于0和小于0时,![]() 的范围,可得函数
的范围,可得函数![]() 的单调区间;
的单调区间;
(Ⅱ)对函数求导,写出函数的导函数等于0的![]() 的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于
的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于![]() 的方程求得结果.
的方程求得结果.
试题解析:
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
![]()
当![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ,
,
即函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() .
.
(Ⅱ)因为![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() ,
,![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
所以最大值1可能的在![]() 或
或![]() 处取得,而
处取得,而![]()
![]()
![]() ,
,
所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
所以最大值1可能在![]() 或
或![]() 处取得,
处取得,
而![]() ,
,
所以![]() ,
,
解得![]() ,与
,与![]() 矛盾.
矛盾.
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾.
,矛盾.
综上所述,![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】下列各组函数表示相同函数的是( )
A.f(x)= ![]() ,g(x)=(
,g(x)=( ![]() )2
)2
B.f(x)=1,g(x)=x2
C.f(x)= ![]() ,g(t)=|t|
,g(t)=|t|
D.f(x)=x+1,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017江西上饶联考】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017重庆二诊】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
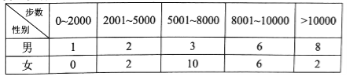
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?

附: ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.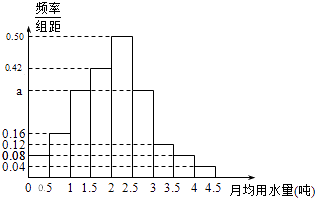
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为 ![]() ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2= ![]()
P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an},{bn}的通项公式.
(2)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【扬州市2016—2017学年度第一学期期末检测】(本小题满分14分)
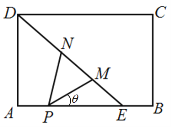
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com