练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图,四楼锥中,平面平面,底面为梯形. ，且与均为正三角形. 为的中点为重心, 与相交于点.

    (1)求证: 平面；

    (2)求三棱锥的体积.

    【答案】（1）见解析（2）

    【解析】试题分析：（1）第（1）问，连交于,连接.证明// ，即证平面. (2)第(2)问，主要是利用体积变换， ,求得三棱锥的体积.

    试题解析：

    （1）方法一：连交于,连接.

    由梯形， 且，知

    又为的中点， 为的重心，∴

    在中， ,故// .

    又平面, 平面,∴ 平面.

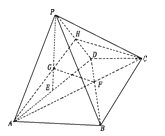
    方法二：过作交PD于N,过F作FM||AD交CD于M,连接MN,

    G为△PAD的重心，

    又ABCD为梯形，AB||CD,

    又由所作GN||AD,FM||AD,得// ，所以GNMF为平行四边形.

    因为GF||MN,

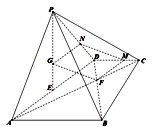
    （2） 方法一:由平面平面， 与均为正三角形， 为的中点

    ∴， ，得平面，且

    由（1）知//平面，∴

    又由梯形ABCD，AB||CD，且，知

    又为正三角形，得，∴，

    得

    ∴三棱锥的体积为.

    方法二: 由平面平面， 与均为正三角形， 为的中点

    ∴， ，得平面，且

    由，∴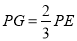

    而又为正三角形，得，得.

    ∴，

    ∴三棱锥的体积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的极坐标方程为ρ2＝.

    (1)若以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，求曲线C的直角坐标方程；

    (2)若P(x，y)是曲线C上的一个动点，求3x＋4y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数有下述四个结论：①若，则；②的图象关于点对称；③函数在上单调递增；④的图象向右平移个单位长度后所得图象关于轴对称.其中所有正确结论的编号是（ ）

    A.①②④B.①②C.③④D.②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法，甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，组成了干支纪年法，其相配顺序为：甲子、乙丑、丙寅…癸酉，甲戌、乙亥、丙子…癸末，甲申、乙酉、丙戌…癸巳，…，共得到个组成，周而复始，循环记录。2014年是“干支纪年法”中的甲午年，那么2020年是“干支纪年法”中的（）

    A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位：千元）对年销售量（单位：）和年利润（单位：千元）的影响，对近年的宣传费，和年销售量的数据作了初步处理，得到下面的散点图及一些统计量的值，表中

    (Ⅰ)根据散点图判断，与，哪一个宜作为年销售量关于年宣传费的回归方程类型（给出判断即可，不必说明理由）；

    (Ⅱ)根据(Ⅰ)的判断结果及表中数据，建立关于的回归方程；

    (Ⅲ)已知这种产品的年利润与，的关系为，根据(Ⅱ)的结果回答下列问题：

    (1)当年宣传费时，年销售量及年利润的预报值时多少？

    (2)当年宣传费为何值时，年利润的预报值最大？

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的准线与轴交于点，过点作圆的两条切线，切点为，且.

    (1)求抛物线的方程；

    (2)若直线是过定点的一条直线，且与抛物线交于两点，过定点作的垂线与抛物线交于两点，求四边形面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】庙会是我国古老的传统民俗文化活动,又称“庙市”或 “节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”（游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”）.今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:

    甲说:“我或乙能中奖”； 乙说:“丁能中奖”；

    丙说:“我或乙能中奖”； 丁说:“甲不能中奖”.

    游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是( )

    A. 甲 B. 乙 C. 丙 D. 丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】重庆市推行“共享吉利博瑞车”服务，租用该车按行驶里程加用车时间收费，标准是“1元/公里0.2元/分钟”．刚在重庆参加工作的小刘拟租用“共享吉利博瑞车”上下班，同单位的邻居老李告诉他：“上下班往返总路程虽然只有10公里，但偶尔开车上下班总共也需花费大约1小时”，并将自己近50天的往返开车的花费时间情况统计如表：

    将老李统计的各时间段频率视为相应概率，假定往返的路程不变，而且每次路上开车花费时间视为用车时间．

    （1）试估计小刘每天平均支付的租车费用（每个时间段以中点时间计算）；

    （2）小刘认为只要上下班开车总用时不超过45分钟，租用“共享吉利博瑞车”为他该日的“最优选择”，小刘拟租用该车上下班2天，设其中有天为“最优选择”，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （Ⅰ）当时，求函数的单调递减区间；

    （Ⅱ）若时，关于的不等式恒成立，求实数的取值范围；

    （Ⅲ）若数列满足， ，记的前项和为，求证： .

    【答案】（I）；（II）；（III）证明见解析.

    【解析】试题分析：（Ⅰ）求出，在定义域内，分别令求得的范围，可得函数增区间， 求得的范围，可得函数的减区间；（Ⅱ）当时，因为，所以显然不成立，先证明因此时， 在上恒成立，再证明当时不满足题意，从而可得结果；（III）先求出等差数列的前项和为，结合（II）可得，各式相加即可得结论.

    试题解析：（Ⅰ）由，得.所以

    令，解得或（舍去），所以函数的单调递减区间为 .

    （Ⅱ）由得，

    当时，因为，所以显然不成立，因此.

    令，则，令，得.

    当时， ， ，∴，所以，即有.

    因此时， 在上恒成立.

    ②当时， ， 在上为减函数，在上为增函数，

    ∴，不满足题意.

    综上，不等式在上恒成立时，实数的取值范围是.

    （III）证明：由知数列是的等差数列，所以

    所以

    由（Ⅱ）得， 在上恒成立.

    所以. 将以上各式左右两边分别相加，得

    .因为

    所以

    所以.

    【题型】解答题
    【/span>结束】
    22

    【题目】已知直线， (为参数， 为倾斜角).以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的直角坐标方程为.

    （Ⅰ）将曲线的直角坐标方程化为极坐标方程；

    （Ⅱ）设点的直角坐标为，直线与曲线的交点为、，求的取值范围.

    查看答案和解析>>

    同步练习册答案