
(本小题满分11分)对于定义域为D的函数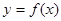 ,如果存在区间
,如果存在区间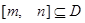 ,同时满足:
,同时满足:
①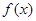 在
在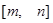 内是单调函数;
内是单调函数;
②当定义域是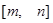 时,
时,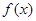 的值域也是
的值域也是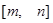 .
.
则称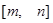 是该函数的“和谐区间”.
是该函数的“和谐区间”.
(1)证明: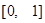 是函数
是函数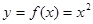 的一个“和谐区间”.
的一个“和谐区间”.
(2)求证:函数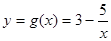 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知函数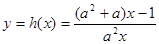 (
(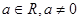 )有“和谐区间”
)有“和谐区间”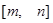 ,当
,当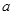 变化时,求出
变化时,求出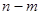 的最大值.
的最大值.
解:(1)区间 是
是 的一个“和谐区间”.
的一个“和谐区间”.
(2)函数 不存在“和谐区间”.
不存在“和谐区间”.
(3)当 时,
时, 取最大值
取最大值 .
.
【解析】本试题主要是结合了函数的单调性和函数的定义域和值域的有关系概念,对于新定义“和谐区间”的理解和灵活的运用。
(1) 在区间
在区间 上单调递增,并且满足第二点又
上单调递增,并且满足第二点又 ,
, ,
, 值域为
值域为 ,故得到结论。
,故得到结论。
(2)假设存在一个区间满足题意,利用反比列函数的性质可知,没有和谐区间。
(3)根据已知条件可知,函数存在和谐区间,那么可以设出区间,再分析函数的单调性,得到定义域和值域的关系,进而得到结论。
解:(1) 在区间
在区间 上单调递增.
上单调递增.
又 ,
, ,
, 值域为
值域为 ,
,
 区间
区间 是
是 的一个“和谐区间”.…………2分
的一个“和谐区间”.…………2分
(2)设 是已知函数定义域的子集.
是已知函数定义域的子集. ,
, 或
或 ,故函数
,故函数 在
在 上单调递增.
上单调递增.
若 是已知函数的“和谐区间”,则
是已知函数的“和谐区间”,则
故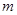 、
、 是方程
是方程 的同号的相异实数根.
的同号的相异实数根.
 无实数根,
无实数根, 函数
函数 不存在“和谐区间”.………………5分
不存在“和谐区间”.………………5分
(3)设 是已知函数定义域的子集.
是已知函数定义域的子集. ,
, 或
或 ,故函数
,故函数 在
在 上单调递增.
上单调递增.
若 是已知函数的“和谐区间”,则
是已知函数的“和谐区间”,则
故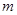 、
、 是方程
是方程 ,即
,即 的同号的相异实数根.
的同号的相异实数根.
 ,
, ,
, 同号,只须
同号,只须 ,即
,即 或
或 时,已知函数有“和谐区间”
时,已知函数有“和谐区间” ,
, ,
,
 当
当 时,
时, 取最大值
取最大值 ………………11分
………………11分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013届浙江省高二下学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分11分) 已知函数 ,其中
,其中 .
.
(1) 当 时,求
时,求 的单调区间;
的单调区间;
(2) 证明:对任意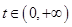 ,
, 在区间
在区间 内存在零点.
内存在零点.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高二上学期期中考试理科数学 题型:解答题
(本小题满分11分)
已知a、b、c为三角形ABC中角A、B、C的对边,且
 ,求这个三角形的最大内角.
,求这个三角形的最大内角.
查看答案和解析>>
科目:高中数学 来源:2010年陕西省西安市铁一中高二下学期期中考试数学(理) 题型:解答题
(本小题满分11分)已知,
 ;
;
(1)试由此归纳出当 时相应的不等式;
时相应的不等式;
(2)试用数学归纳法证明你在第(1)小题得到的不等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com