
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
【答案】![]() Ⅰ
Ⅰ![]() 详见解析;
详见解析;![]() Ⅱ
Ⅱ![]() ①
①![]() ,②
,②![]() 或
或![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 可以通过已知证明出
可以通过已知证明出![]() 平面PAB,这样就可以证明出
平面PAB,这样就可以证明出![]() ;
;
![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为![]() 、平面PCD的法向量
、平面PCD的法向量![]() ,利用空间向量的数量积,求出二面角
,利用空间向量的数量积,求出二面角![]() 的大小;
的大小;
![]() 求出平面PBC的法向量,利用线面角的公式求出
求出平面PBC的法向量,利用线面角的公式求出![]() 的值.
的值.
证明:![]() Ⅰ
Ⅰ![]() 在图1中,
在图1中,![]() ,
,![]() ,
,
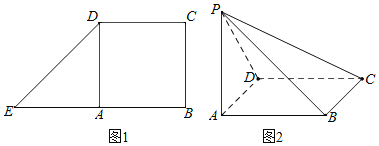
![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() ,
,![]() ,
,
当![]() 沿AD折起时,
沿AD折起时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 平面PAB,
平面PAB,
又![]() 平面PAB,
平面PAB,![]() .
.
解:![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于![]() 平面ABCD
平面ABCD
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]()
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
设平面PBC的法向量为![]() y,
y,![]() ,
,
则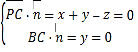 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
设平面PCD的法向量![]() b,
b,![]() ,
,
则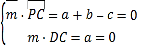 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,可知为钝角,
,可知为钝角,
则![]() ,
,![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
![]() 设AM与面PBC所成角为
设AM与面PBC所成角为![]() ,
,
![]() 0,
0,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
平面PBC的法向量![]() 0,
0,![]() ,
,
![]() 直线AM与平面PBC所成的角为
直线AM与平面PBC所成的角为![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点B(﹣1,0),设不垂直于x轴的直线与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)满足x2f′(x)+2xf(x)= ![]() ,f(2)=
,f(2)= ![]() ,则x>0时,f(x)( )
,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ ![]() 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣ ![]() .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
| 30 |
| |
|
|
| |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为
地区当中“非常满意”的观众的概率为![]() ,且
,且![]() .
.
(Ⅰ)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少;
地区的人数各是多少;
(Ⅱ)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
(Ⅲ)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
|
|
附:参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2 ![]()
(1)求数列{an}的通项公式an;
(2)令b ![]() ,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有
,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com