
已知函数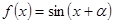 ,
, 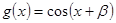 ,
,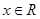 ,
,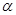 、
、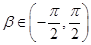 .
.
(Ⅰ)若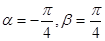 ,判断
,判断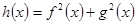 的奇偶性;
的奇偶性;
(Ⅱ) 若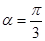 ,
,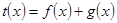 是偶函数,求
是偶函数,求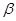 ;
;
(Ⅲ)是否存在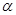 、
、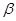 ,使得
,使得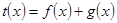 是奇函数但不是偶函数?若存在,试确定
是奇函数但不是偶函数?若存在,试确定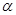 与
与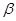 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
(Ⅰ)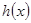 是非奇非偶函数.(Ⅱ)
是非奇非偶函数.(Ⅱ)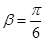 ;(Ⅲ)存在
;(Ⅲ)存在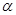 、
、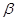 满足
满足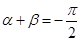 时,
时,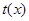 是奇函数但不是偶函数.
是奇函数但不是偶函数.
【解析】
试题分析:(Ⅰ) 方法一(定义法):
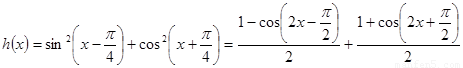
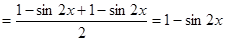 . 2分
. 2分
所以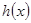 是非奇非偶函数. 3分
是非奇非偶函数. 3分
方法二(特殊值法):由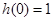 知
知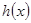 不是奇函数. 1分
不是奇函数. 1分
又由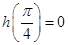 ,
,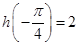 知
知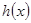 不是偶函数. 2分
不是偶函数. 2分
所以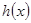 是非奇非偶函数. 3分
是非奇非偶函数. 3分
(Ⅱ) 方法一(定义法):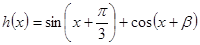 ,
,
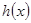 偶函数,
偶函数,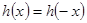 ,
,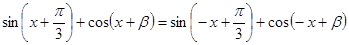
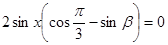 , 5分
, 5分
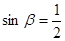 ,
,
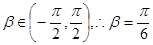 . 6分
. 6分
方法二(特殊值法):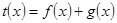 为偶函数
为偶函数
所以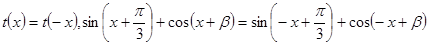
 所以
所以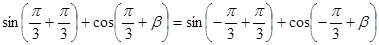 5分
5分
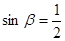 ,
,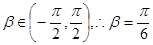 ,经验证
,经验证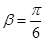 满足题意. 6分
满足题意. 6分
(Ⅲ)方法一:假设存在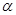 、
、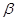 ,使得
,使得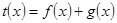 是奇函数.
是奇函数.
由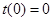 得,
得,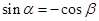 ,所以
,所以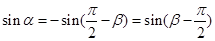 .
.
由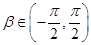 知,
知,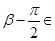
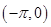 .
.
又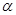
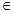
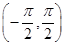 ,故
,故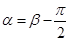 或
或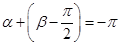 ,
,
即 或
或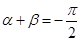 .
8分
.
8分
当 时,
时,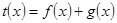 =
= +
+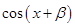
= +
+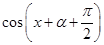 =
= -
- =0,
=0,
此时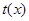 既是奇函数又是偶函数.不合题意,舍去. 9分
既是奇函数又是偶函数.不合题意,舍去. 9分
当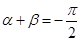 时,
时,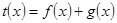 =
= +
+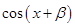
= +
+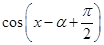 =
= -
-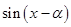 =
=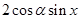
此时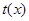 是奇函数但不是偶函数.
是奇函数但不是偶函数.
综上,存在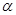 、
、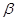 满足
满足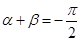 时,
时,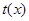 是奇函数但不是偶函数.
10分
是奇函数但不是偶函数.
10分
方法二:假设存在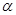 、
、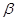 ,使得
,使得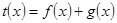 是奇函数.
是奇函数.
由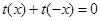 得,
得,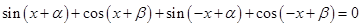
化简整理得,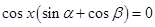 ,从而
,从而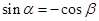 .下同方法一.
.下同方法一.
考点:三角函数的奇偶性;二倍角公式;三角函数的综合应用。
点评:(1)此题主要考查三角函数的奇偶性。判断一个函数奇偶性的步骤:一求函数的定义域,看定义域是否关于原点对称;二判断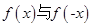 。有时,若
。有时,若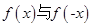 的关系不好判断时,可以根据定义域进行化简。(2) 若函数
的关系不好判断时,可以根据定义域进行化简。(2) 若函数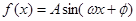 为偶函数,则
为偶函数,则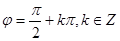 ;若函数
;若函数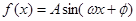 为奇函数,则
为奇函数,则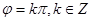 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 24 |
| 5π |
| 24 |
| π |
| 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11π |
| 6 |
| ||
| 2 |
| 3 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| xn+2 | xn-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com