
【题目】在![]() 中,三内角A,B,C的对边分别为a,b,c.
中,三内角A,B,C的对边分别为a,b,c.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,且
,且![]() 为钝角,证明:
为钝角,证明: ![]() ,并求
,并求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,(2)
,(2)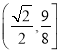
【解析】试题分析:
(1)由题意结合正弦定理可得![]() 或
或![]() ,结合两角和差正余弦公式可得
,结合两角和差正余弦公式可得![]() ;
;
(2)利用题意得到关于sinA的二次函数,结合二次函数的性质可得![]() 的取值范围是
的取值范围是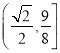 .
.
试题解析:
(1)由正弦定理可得![]() ,
,
∵c![]() ,A=45°,a=2,
,A=45°,a=2,
∴sinC=![]() ,
,
∴C=60°或120°,
由正弦定理可得![]()
当C=60°,sinB=sin(A+C)=sin45°cos60°+cos45°sin60°=![]()
∴b=![]() ,
,
当C=120°,sinB=sin(A+C)=sin45°cos120°+cos45°sin120°=![]()
∴b=![]() ,
,
(2)由题意得a=btanA,
∴由正弦定理得![]() ,则sinB=cosA,
,则sinB=cosA,
∵B为钝角,∴![]() ,
,
∴BA=![]() ;
;
∴C=π(A+B)=π(A+![]() +A)=
+A)= ![]() 2A>0,
2A>0,
∴A∈(0, ![]() ),
),
∴sinA+sinC=sinA+sin(![]() 2A)=sinA+cos2A=sinA+12sin/span>2A=2(sinA
2A)=sinA+cos2A=sinA+12sin/span>2A=2(sinA![]() )2+
)2+![]() ,
,
∵A∈(0, ![]() ),∴0<sinA<
),∴0<sinA<![]() ,
,
∴由二次函数可知, ![]() ,
,
∴sinA+sinC的取值范围为 .
.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
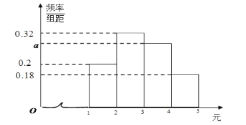
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
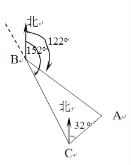
【题目】如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为![]() 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为![]() .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为![]() .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在区间![]() 上的函数
上的函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() 成立,那么称函数
成立,那么称函数![]() 在区间
在区间![]() 上可被
上可被![]() 替代,
替代,![]() 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:
①![]() 在区间
在区间![]() 上可被
上可被![]() 替代;
替代;
②![]() 可被
可被![]() 替代的一个“替代区间”为
替代的一个“替代区间”为![]() ;
;
③![]() 在区间
在区间![]() 可被
可被![]() 替代,则
替代,则![]() ;
;
④![]() (
(![]() ),
),![]() (
(![]() ),则存在实数
),则存在实数![]() (
(![]() ),使得
),使得![]() 在区间
在区间![]() 上被
上被![]() 替代; 其中真命题有 .
替代; 其中真命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() 满足
满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 方程
方程![]() 有两个不等实根;
有两个不等实根;
若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求
”为真命题,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com