Question

直线l垂直于梯形ABCD的两腰AB和CD，直线m垂直于AD和BC，则l与m的位置关系是（ ）
A．相交
B．平行
C．异面
D．不确定

Answer 1

【答案】分析：作出如图所示的直四棱柱，分别找出或作出符合条件的直线l、m，即可判断出结论．
解答：解：如图所示：直四棱柱ABCD-A₁B₁C₁D₁中，
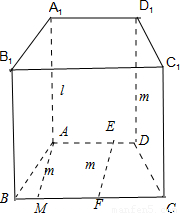
取棱AA₁为直线l，则l⊥AB，l⊥CD．
①若取棱D₁D为直线m，则m⊥AD，m⊥BC，满足条件，此时m∥l；
②过点A作AM⊥BC，∵AD∥BC，∴AM⊥AD，取直线AM为m，则满足条件，此时l与m相交；
③过线段AD上除去点A以外的点E作EF∥AM，则EF⊥AD，EF⊥BC，取EF为直线m，则满足条件，此时l与m为异面直线．
综上可知：l与m的位置关系是平行、相交或异面直线，因此其位置关系不确定．
故选D．
点评：作出直四棱柱，熟练掌握空间中直线的位置关系是解题的关键．