
����Ŀ����ͼ��OM��ON�����������ߣ�QΪ����һ��С����AΪ������OM�ϵ�һ����ͷ����֪![]() ��
��![]() ��Q��������OM��ON�ľ���ֱ�Ϊ3 km��
��Q��������OM��ON�ľ���ֱ�Ϊ3 km��![]() km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q��
km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q��
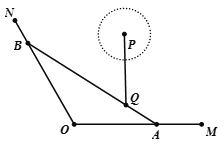
��1����ˮ��������AB�ij���
��2����С�������������С��6 km���ĺ�����һ��Բ��ǿˮ��P����ˮ������t hʱ�İ뾶Ϊ![]() ��aΪ������ij�������ǿˮ����ʼ����ʱ��һ������
��aΪ������ij�������ǿˮ����ʼ����ʱ��һ������![]() km/h���ٶ�����ͷA������ͷB����ʵ��a��ʲô��Χȡֵʱ��ǿˮ�����Შ�����ֵĺ��У�
km/h���ٶ�����ͷA������ͷB����ʵ��a��ʲô��Χȡֵʱ��ǿˮ�����Შ�����ֵĺ��У�
���𰸡���1��![]() ��2��
��2��![]()
��������
���⣨1������������ֱ������ϵ��Ϊ�����ʾ��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����Q��������ON�ľ���Ϊ
����Q��������ON�ľ���Ϊ![]() km����
km����![]() �����
�����![]() ��������ֱ�߽����
��������ֱ�߽����![]() �������������빫ʽ��
�������������빫ʽ��![]() ��2����������һ������ʽ��������⣺��
��2����������һ������ʽ��������⣺��![]() Сʱʱ���������߶�
Сʱʱ���������߶�![]() �ϵĵ�
�ϵĵ�![]() ����
����![]() ������ʽ����������������ñ������뽫��ת��Ϊ��Ӧ������ֵ���⣺
������ʽ����������������ñ������뽫��ת��Ϊ��Ӧ������ֵ���⣺![]()
�����������1���Ե�![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() Ϊ
Ϊ![]() �ᣬ����ֱ������ϵ��ͼ��ʾ��
�ᣬ����ֱ������ϵ��ͼ��ʾ��

��������ã�![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��![]() ����
����![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����
����![]() �� ��
�� ��![]() ��
��![]() ��
��![]() ����
����![]() ����ˮ��������
����ˮ��������![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
��2�������������ǿˮ��Բ![]() ��������ɵ�P��3��9��������
��������ɵ�P��3��9��������![]() Сʱʱ���������߶�
Сʱʱ���������߶�![]() �ϵĵ�
�ϵĵ�![]() ������
������![]() ����
����![]() ��ǿˮ�����Შ�����ֵĺ��м�
��ǿˮ�����Შ�����ֵĺ��м�![]()
![]() ����
����![]() ʱ ��
ʱ ��![]() ��
��![]()
![]() .
.![]() ��
��![]() �����ҽ���
�����ҽ���![]() ʱ�Ⱥų��������ԣ���
ʱ�Ⱥų��������ԣ���![]() ʱ
ʱ![]() ��������༴ǿˮ�����Შ�����ֵĺ��У�
��������༴ǿˮ�����Შ�����ֵĺ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2����![]() ʱ��֤��������
ʱ��֤��������![]() ֻ��һ����㣻
ֻ��һ����㣻
��3��������![]() �ļ���ֵ����
�ļ���ֵ����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() ���������ʵ��
���������ʵ��![]() ʹ��
ʹ��![]() ����ô��
����ô��![]() Ϊ
Ϊ![]() �����Ժ���.
�����Ժ���.
��1������������麯�����ж�![]() �Ƿ�ֱ�Ϊ
�Ƿ�ֱ�Ϊ![]() �����Ժ�������˵�����ɣ�
�����Ժ�������˵�����ɣ�
��һ�飺![]()
�ڶ���:��![]()
��2����![]() �����Ժ���Ϊ
�����Ժ���Ϊ![]() .����ʽ
.����ʽ![]() ��
��![]() ���н⣬��ʵ��
���н⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��ȡ
��ȡ![]() .���Ժ���
.���Ժ���![]() ͼ�����͵�Ϊ
ͼ�����͵�Ϊ![]() .������������ʵ��
.������������ʵ��![]() ��
��![]() .�����Ƿ�������ij���
.�����Ƿ�������ij���![]() ��ʹ
��ʹ![]() �������������ڣ�������
�������������ڣ�������![]() ��ֵ����������ڣ���˵������.
��ֵ����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ��
��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ��
��![]() ��
��
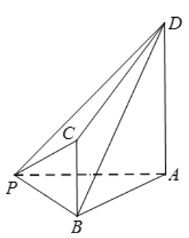
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ��
��![]() �ϵ����ݼ�����
�ϵ����ݼ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() ��������
��������![]() ���������ߣ�֤����
���������ߣ�֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() �Ľ�����x���ϣ�������Ϊ
�Ľ�����x���ϣ�������Ϊ![]() ����������
����������![]() ���ĸ����������ı��ε����Ϊ40.
���ĸ����������ı��ε����Ϊ40.
��1������![]() �ı����̣�
�ı����̣�
��2��������M������һ�㵽![]() ���ҽ���ľ���������ֱ��
���ҽ���ľ���������ֱ��![]() �ľ�����ȣ�ֱ��
�ľ�����ȣ�ֱ��![]() ����
����![]() ���¶�����Ҷ��㣬
���¶�����Ҷ��㣬![]() ��ֱ��
��ֱ��![]() ������M�ཻ�ڵ�P��Q����P�ڵ�һ�����ڣ���Q�ڵ��������ڣ�����
������M�ཻ�ڵ�P��Q����P�ڵ�һ�����ڣ���Q�ڵ��������ڣ�����![]() ���¶�����B���϶�����D����
���¶�����B���϶�����D����![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У���ǰn���Sn��n2��2n+b��1��{bn}�ǵȱ����У���ǰn���Tn![]() ��������{ bn +an}��ǰ5���Ϊ��������
��������{ bn +an}��ǰ5���Ϊ��������
A.37B.-27C.77D.46
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶�����Ʒ��Ϊ�˳��³ߴ��������ѡ��15��־Ը�ߣ��������ߺͱ�չ���в�������λ�����ף�����ͼΪѡȡ��15��־Ը���������չ������ͼ����ͼΪ�������չ����Ӧ��ɢ��ͼ���������ع鷽��Ϊ![]() �����½����в���ȷ��Ϊ
�����½����в���ȷ��Ϊ


A. 15��־Ը�����ߵļ���С�ڱ�չ�ļ���
B. 15��־Ը�����ߺͱ�չ������ع�ϵ��
C. �ɹ�������Ϊ190�����˱�չ��ԼΪ189.65���ף�
D. �������10�������˱�չ�����11.6���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ������
������![]() ������
������![]() ��
��![]() Ϊ
Ϊ![]() ���е�.
���е�.
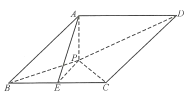
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ����ƽ��
����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ.
���������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com