
【题目】设函数 ![]() ,
, ![]() 是其函数图象的一条对称轴. (Ⅰ)求ω的值;
是其函数图象的一条对称轴. (Ⅰ)求ω的值;
(Ⅱ)若f(x)的定义域为 ![]() ,值域为[﹣1,5],求a,b的值.
,值域为[﹣1,5],求a,b的值.
【答案】解:(Ⅰ)∵函数 ![]() =
= ![]() +
+ ![]() cos(2ωx)+
cos(2ωx)+ ![]() asin(2ωx)=b+
asin(2ωx)=b+ ![]() +acos(2ωx﹣
+acos(2ωx﹣ ![]() ), 再由
), 再由 ![]() 是其函数图象的一条对称轴,可得 2ω
是其函数图象的一条对称轴,可得 2ω ![]() ﹣
﹣ ![]() =kπ,k∈z,ω=3k+1,
=kπ,k∈z,ω=3k+1,
∴ω=1.
(Ⅱ)由(1)可得 f(x)=b+ ![]() +acos(2x﹣
+acos(2x﹣ ![]() ),再根据x∈
),再根据x∈ ![]() ,可得 2x﹣
,可得 2x﹣ ![]() ∈[﹣π,
∈[﹣π, ![]() ],故cos(2x﹣
],故cos(2x﹣ ![]() )∈[﹣1,1].
)∈[﹣1,1].
再由函数f(x)的值域为[﹣1,5],可得 ①  ,或②
,或②  .
.
由①可得 ![]() ,解②可得
,解②可得  .
.
综上可得 ![]() ,或
,或  .
.
【解析】(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为 b+ ![]() +acos(2ωx﹣
+acos(2ωx﹣ ![]() ),再由
),再由 ![]() 是其函数图象的一条对称轴,可得 2ω
是其函数图象的一条对称轴,可得 2ω ![]() ﹣
﹣ ![]() =kπ,k∈z,由此求得ω 的值.(Ⅱ)由(1)可得 f(x)=b+
=kπ,k∈z,由此求得ω 的值.(Ⅱ)由(1)可得 f(x)=b+ ![]() +acos(2x﹣
+acos(2x﹣ ![]() ),再根据x∈
),再根据x∈ ![]() ,可得cos(2x﹣
,可得cos(2x﹣ ![]() )∈[﹣1,1].再由函数f(x)的值域为[﹣1,5],可得 ①
)∈[﹣1,1].再由函数f(x)的值域为[﹣1,5],可得 ①  ,或②
,或②  ,由此求得a、b的值.
,由此求得a、b的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】空间四边形ABCD的对角线AC=10,BD=6,M、N分别为AB、CD的中点,MN=7,则异面直线AC和BD所成的角等于( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),且直线
不重合),且直线![]() 与
与![]() 轴的交于点
轴的交于点![]() ,试问
,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
(Ⅰ)求证:MN∥平面PAD;
(Ⅱ)求二面角B﹣AM﹣C的大小;
(Ⅲ)在BC上是否存在点E,使得EN⊥平面AMN?若存在,求 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,有下列4个命题:
,有下列4个命题:
①若![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
②![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若![]() 为奇函数,且
为奇函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
其中正确的命题为 .(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
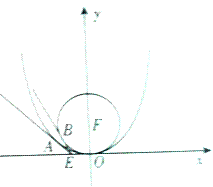
【题目】如图所示,抛物线C:x2=2py(p>0),其焦点为F,C上的一点M(4,m)满足|MF|=4.
(1)求抛物线C的标准方程;
(2)过点E(﹣1,0)作不经过原点的两条直线EA,EB分别与抛物线C和圆F:x2+(y﹣2)2=4相切于点A,B,试判断直线AB是否经过焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com