
(本题满分12分)已知函数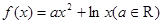
(Ⅰ)当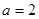 时,求
时,求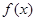 在区间
在区间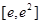 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)如果函数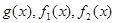 在公共定义域D上,满足
在公共定义域D上,满足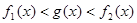 ,
,
那么就称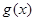 为
为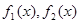 的“伴随函数”.已知函数
的“伴随函数”.已知函数
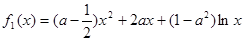 ,
,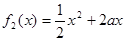 .若在区间
.若在区间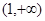 上,
上,
函数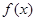 是
是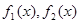 的“伴随函数”,求
的“伴随函数”,求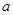 的取值范围.
的取值范围.
解:(Ⅰ)当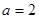 时,
时,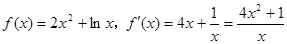 ; ----------1分
; ----------1分
对于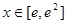 ,有
,有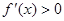 ,∴
,∴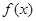 在区间
在区间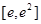 上为增函数,
上为增函数,
∴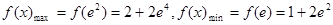 .
-----------------3分
.
-----------------3分
(Ⅱ)在区间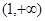 上,函数
上,函数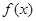 是
是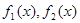 的“伴随函数”,则
的“伴随函数”,则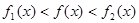 ,令
,令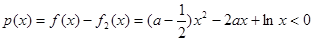 对
对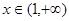 恒成立, ------4分
恒成立, ------4分
且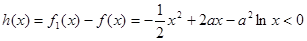 对
对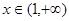 恒成立, ------5分
恒成立, ------5分
∵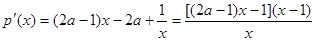 (*)
--------------6分
(*)
--------------6分
①若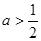 ,令
,令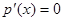 ,得极值点
,得极值点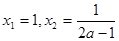 ,当
,当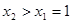 ,即
,即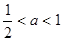 时,在
时,在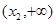 上有
上有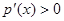 ,
--------------7分
,
--------------7分
此时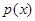 在区间
在区间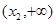 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有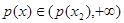 ,不合题意;
,不合题意;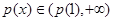 ,也不合题意;
-----------------8分
,也不合题意;
-----------------8分
②若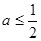 ,则有
,则有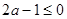 ,此时在区间
,此时在区间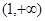 上恒有
上恒有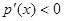 ,
,
从而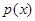 在区间
在区间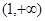 上是减函数;
上是减函数;
要使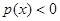 在此区间上恒成立,只需满足
在此区间上恒成立,只需满足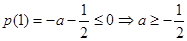 ,所以
,所以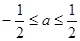 .
-----------------9分
.
-----------------9分
又因为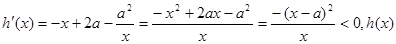 在
在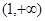 上是减函数.
上是减函数.
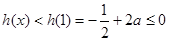 ,所以
,所以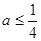 .
.
综合可知 的取值范围是
的取值范围是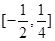 .
-----------------10分
.
-----------------10分
另解:(接在(*)号后)
先考虑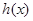 ,
,
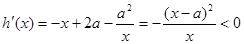 ,--------------8分
,--------------8分
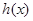 在
在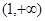 上递减,只要
上递减,只要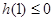 ,即
,即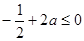 ,解得
,解得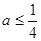 .-----------7分
.-----------7分
而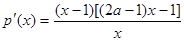 对
对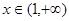 ,且
,且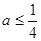 有
有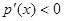 . --------8分
. --------8分
只要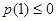 ,即
,即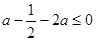 ,解得
,解得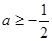 ,所以
,所以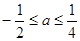 ,--------9分
,--------9分
即 的取值范围是
的取值范围是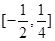 .
-----------------10分
.
-----------------10分
【解析】略


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:安徽省合肥一中、六中、一六八中学2010-2011学年高二下学期期末联考数学(理 题型:解答题
(本题满分12分)已知△ 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 的大小;(2)若
的大小;(2)若 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:2011届本溪县高二暑期补课阶段考试数学卷 题型:解答题
(本题满分12分)已知各项均为正数的数列 ,
, 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳市高三调研检测数学理卷 题型:解答题
(本题满分12分)
已知椭圆 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点.
(1)若 ,且
,且 ,
, ,求
,求 、
、 的坐标;
的坐标;
(2)在(1)的条件下,过动点 作以
作以 为圆心、以1为半径的圆的切线
为圆心、以1为半径的圆的切线 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二上学期10月月考理科数学卷 题型:解答题
(本题满分12分)已知椭圆 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量
(1)求椭圆的离心率
(2)设Q是椭圆上任意一点, 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com