
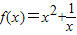 在(1,+∞)上的单调性,并用定义法加以证明;
在(1,+∞)上的单调性,并用定义法加以证明;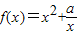 在区间(1,+∞)上的单调递增,求实数a的取值范围.
在区间(1,+∞)上的单调递增,求实数a的取值范围.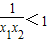 ∴
∴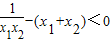 …(5分)
…(5分)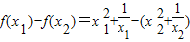
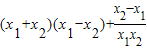
 …(7分)
…(7分)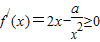 在区间(1,+∞)上恒成立,∴a≤2x3在区间(1,+∞)上恒成立,∴a≤2.…(16分)
在区间(1,+∞)上恒成立,∴a≤2x3在区间(1,+∞)上恒成立,∴a≤2.…(16分)

科目:高中数学 来源: 题型:
| a |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若任意的
,若任意的![]() ,当
,当![]() 时,总有
时,总有![]() .
.
(1)判断函数![]() 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,其中
恒成立,其中![]() (
(![]() 是常数),求实数
是常数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高一第四次月考数学试卷(解析版) 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
(1)判断函数 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;
(2)试证明:设 ,若
,若 在
在 上分别以
上分别以 为上界,
为上界,
求证:函数 在
在 上以
上以 为上界;
为上界;
(3)若函数 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数,
求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届北京五中高一第一学期期中考试数学试卷 题型:解答题
定义在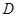 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是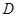 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
(1)判断函数 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;
(2)试证明:设 ,若
,若 在
在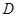 上分别以
上分别以 为上界,
为上界,
求证:函数 在
在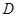 上以
上以 为上界;
为上界;
(3)若函数 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数,
求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com