
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)借助题设条件建立方程组求解;(II)借助题设运用直线与椭圆的位置关系推证和探求.
试题解析:
(I)由题意得:![]() ,
,![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .………………5分
.………………5分
(II)存在符合条件的圆,且此圆的方程为![]() .
.
证明如下:假设存在符合条件的圆,并设此圆的方程为![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() .
.
由方程组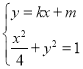 得
得![]() .
.
∵直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,
有且仅有一个公共点,
∴![]() ,即
,即![]() .
.
由方程组 得
得![]() ,
,
则![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
设直线![]() 的斜率分别为
的斜率分别为![]() ,
,
∴![]()
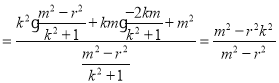 ,将
,将![]() 代入上式,
代入上式,
得![]() .
.
要使得![]() 为定值,则
为定值,则![]() ,即
,即![]() ,代入
,代入![]() 验证知符合题意.
验证知符合题意.
∴当圆的方程为![]() 时,圆与
时,圆与![]() 的交点
的交点![]() 满足
满足![]() 为定值
为定值![]() .
.
当直线![]() 的斜率不存在时,由题意知
的斜率不存在时,由题意知![]() 的方程为
的方程为![]() .
.
此时,圆![]() 与
与![]() 的交点
的交点![]() 也满足
也满足![]() .
.
综上,当圆的方程为![]() 时,
时,
圆与![]() 的交点
的交点![]() 满足直线
满足直线![]() 的斜率之积为定值
的斜率之积为定值![]() .……………………12分
.……………………12分


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知随机变量X~N(μ,σ2),且其正态曲线在(-∞,80)上是增函数,在(80,+∞)上为减函数,且P(72≤X≤88)=0.682 6.
(1)求参数μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块![]() 的一角
的一角![]() 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角![]() 为
为![]() ,
,![]() 的长度均大于
的长度均大于![]() 米,现在边界
米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
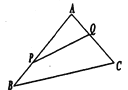
(1)若围墙![]() 总 长度为
总 长度为![]() 米,如何围可使得三角形地块
米,如何围可使得三角形地块![]() 的面积最大?
的面积最大?
(2)已知![]() 段围墙高
段围墙高![]() 米,
米,![]() 段围墙高
段围墙高![]() 米,造价均为每平方米
米,造价均为每平方米![]() 元.若围围墙用了
元.若围围墙用了![]() 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
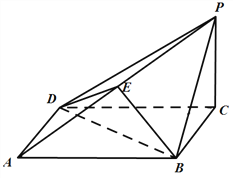
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,点
为正方形,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ) 设![]() ,试判断平面
,试判断平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,写出
能否成立;若成立,写出![]() 的一个值(只需写出结论).
的一个值(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是
A. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点;
内的任意一条直线都没有公共点;
B. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都平行;
内的任意一条直线都平行;
C. 若直线![]() 上有无数个点不在平面
上有无数个点不在平面 ![]() 内,则
内,则![]() ;
;
D. 如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A,B,C的对边分别是a,b,c,且b(sinB-sinC)+(c-a)(sinA+sinC)=0.
(Ⅰ)求角A的大小;
(Ⅱ)若![]() ,
,![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com