
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
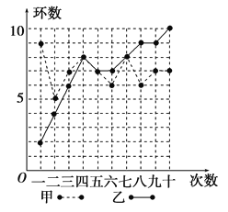
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
参考公式:![]() .
.
【答案】(1)详见解析;(2)①甲成绩比乙稳定;②乙成绩比甲好些;③乙更有潜力.
【解析】
(1)根据统计图列举出甲、乙两人各射击![]() 次中靶环数,并计算出乙射击
次中靶环数,并计算出乙射击![]() 次中靶环数的平均数、方差以及命中
次中靶环数的平均数、方差以及命中![]() 环及
环及![]() 环以上的次数,由此可完善表格;
环以上的次数,由此可完善表格;
(2)①根据表格中的数据甲、乙两人的平均数和方差的大小,由此可得出结论;
②根据表格中的数据甲、乙两人的平均数和命中![]() 环及
环及![]() 环以上的次数的大小,由此可得出结论;
环以上的次数的大小,由此可得出结论;
③根据甲、乙两人射击命中环数的波动情况可得出结论.
解:(1)由列联表中数据,计算由题图,知:
甲射击10次中靶环数分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
将它们由小到大排列为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
乙射击![]() 次中靶环数分别为
次中靶环数分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
将它们由小到大排列为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(1)![]()
![]() (环),
(环),
![]()
![]() .
.
填表如下:
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
|
|
|
(2)①![]() 平均数相同,
平均数相同,![]() ,
,![]() 甲成绩比乙稳定;
甲成绩比乙稳定;
②![]() 平均数相同,命中
平均数相同,命中![]() 环及
环及![]() 环以上的次数甲比乙少,
环以上的次数甲比乙少,![]() 乙成绩比甲好些;
乙成绩比甲好些;
③甲成绩在平均数上下波动;而乙处于上升势头,从第三次以后就没有比甲少的情况发生,乙更有潜力.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】某快递网点收取快递费用的标准是重量不超过![]() 的包裹收费10元,重量超过
的包裹收费10元,重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
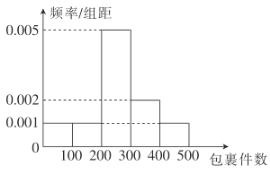
(1)求这60天每天包裹数量的平均数和中位数;
(2)该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润,剩余的作为其他费用.已知该网点有工作人员3人,每人每天工资100元,以样本估计总体,试估计该网点每天的利润有多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
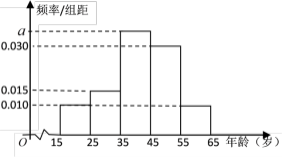
(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 、
、![]() 是
是![]() 上两点.若
上两点.若![]() ,且线段
,且线段![]() 的中点到
的中点到![]() 轴的距离等于
轴的距离等于![]() .
.
(1)求![]() 的值;
的值;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点且在
两点且在![]() 轴的截距为负,过
轴的截距为负,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() .
.
(i)证明:直线![]() 恒过定点,并求出该定点的坐标;
恒过定点,并求出该定点的坐标;
(ii)求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com