Question

【题目】已知椭圆的四个顶点围成的菱形的面积为，椭圆的一个焦点为.

（1）求椭圆的方程；

（2）若，为椭圆上的两个动点，直线，的斜率分别为，，当时，的面积是否为定值？若为定值，求出此定值；若不为定值，说明理由.

Answer 1

【答案】（1）（2）是，定值.

【解析】

（1）由题设条件，列出方程组，结合，求得的值，即可求解.

（2）设，，当直线的斜率存在时，设方程为，联立方程组，结合根与系数的关系和弦长公式，及三角形的面积公式，求得三角形的面积；当直线的斜率不存在时，结合椭圆的对称性和三角形的面积公式，即可求解.

（1）由椭圆的四个顶点围成的菱形的面积为，椭圆的一个焦点为，

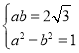可得，，即，解得，，

故椭圆的方程为.

（2）设，，

当直线的斜率存在时，设方程为，

由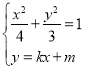，消可得，，

则，即，

且，，

所以

.

又由点到直线的距离，

所以.

又因为，

所以，

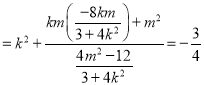化简整理可得，满足，

代入，

当直线的斜率不存在时，由于，

考虑到，关于轴对称，不妨设，，

则点，的坐标分别为，，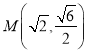

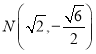此时，

综上可得，的面积为定值.