
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
【答案】
(1)解:因为f(x)是奇函数,所以f(0)=0 ![]() =0,解得b=1,
=0,解得b=1,
f(x)= ![]() ,又由f(1)=﹣f(﹣1)
,又由f(1)=﹣f(﹣1) ![]() ,解得a=2
,解得a=2
(2)证明:由(1)可得:f(x)= ![]() =
= ![]() .
.
x1<x2,∴ ![]() >0,
>0,
则f(x1)﹣f(x2)= ![]() =
= ![]() >0,
>0,
∴f(x1)>f(x2).
∴f(x)在R上是减函数
(3)解:∵函数f(x)是奇函数.
∴f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x)成立,
∵f(x)在R上是减函数,∴kx2<1﹣2x,
∴对于任意 ![]() 都有kx2<1﹣2x成立,
都有kx2<1﹣2x成立,
∴对于任意 ![]() 都有k<
都有k< ![]() ,
,
设g(x)= ![]() ,
,
∴g(x)= ![]() =
= ![]() ,
,
令t= ![]() ,t∈[
,t∈[ ![]() ,2],
,2],
则有 ![]() ,∴g(x)min=g(t)min=g(1)=﹣1
,∴g(x)min=g(t)min=g(1)=﹣1
∴k<﹣1,即k的取值范围为(﹣∞,﹣1)
【解析】(1)直接根据函数是奇函数,满足f(﹣x)=﹣f(x),把x=0,和x=1代入,即可得到关于a,b的两个等式,解方程组求出a,b的值(2)利用减函数的定义即可证明.(3)f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x),即k< ![]() 成立,设g(x)=
成立,设g(x)= ![]() ,
,
换元使之成为二次函数,再求最小值.


科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知椭圆C: ![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆的两个焦点,
是椭圆的两个焦点, ![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的周长是
的周长是![]() .
.
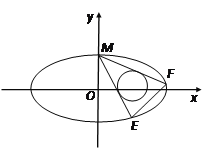
(1)求椭圆C的方程;
(2)设圆T: ![]() ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在![]() 轴上移动且
轴上移动且![]() 时,求EF的斜率的取值范围.
时,求EF的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产![]() 个机器人模型,并对生产的机器人进行编号:
个机器人模型,并对生产的机器人进行编号: ![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的机器人样本,试验小组对
的机器人样本,试验小组对![]() 个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
分组 | 机器人数 | 频率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)补全频率分布表,画出频率分布直方图;
(2)若随机抽的第一个号码为![]() ,这
,这![]() 个机器人分别放在
个机器人分别放在![]() 三个房间,从
三个房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,求
房间,求![]() 房间被抽中的人数是多少?
房间被抽中的人数是多少?
(3)从动作个数不低于![]() 的机器人中随机选取
的机器人中随机选取![]() 个机器人,该
个机器人,该![]() 个机器人中动作个数不低于
个机器人中动作个数不低于![]() 的机器人记为
的机器人记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中,
中, ![]() 是椭圆的左、右焦点,过
是椭圆的左、右焦点,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 的周长为8,离心率为
的周长为8,离心率为![]() .
.
(1)求椭圆方程;
(2)若弦![]() 的斜率不为0,且它的中垂线与
的斜率不为0,且它的中垂线与![]() 轴交于
轴交于![]() ,求
,求![]() 的纵坐标的范围;
的纵坐标的范围;
(3)是否在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,且f(﹣2)=3,f(﹣1)=f(1).
,且f(﹣2)=3,f(﹣1)=f(1).
( I)求f(x)的解析式;
( II)画出f(x)的图象(不写过程)并求其值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若用![]() 代换曲线
代换曲线![]() 的普通方程中的
的普通方程中的![]() 得到曲线
得到曲线![]() 的方程,若
的方程,若![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(1﹣ ![]() ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( ![]() )1008>
)1008> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知映射f:A→B,其中A=B=R,对应法则f:x→y=( ![]() )
) ![]() ,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
A.(﹣∞,2]
B.[2,+∞)
C.(2,+∞)
D.(0,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com