
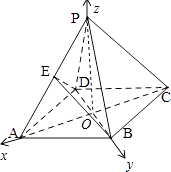
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
【答案】
(1)证明:设AC,BD交点为O,连结PO.则O为正方形ABCD的中心,
∴PO⊥平面ABCD.∵BD平面ABCD,
∴PO⊥BD.
∵四边形ABCD是正方形,∴BD⊥AC.
又AC平面PAC,PO平面PAC,AC∩PO=O,
∴BD⊥平面PAC,又BD平面EBD,
∴平面EBD⊥平面PAC.
(2)解:以O为原点,以OA,OB,OP为坐标轴建立空间直角坐标系,
∵正四棱锥的棱长为4,∴OA=OB=OD=2 ![]() ,OP=
,OP= ![]() =2
=2 ![]() .
.
∴A(2 ![]() ,0,0),B(0,2
,0,0),B(0,2 ![]() ,0),P(0,0,2
,0),P(0,0,2 ![]() ),∴E(
),∴E( ![]() ,0,
,0, ![]() ).
).
∴ ![]() =(
=( ![]() ,﹣2
,﹣2 ![]() ,
, ![]() ).
).
显然x轴⊥平面PBD.∴ ![]() =(1,0,0)是平面PBD的一个法向量,
=(1,0,0)是平面PBD的一个法向量,
∴ ![]() =
= ![]() ,|
,| ![]() |=1,|
|=1,| ![]() |=2
|=2 ![]() .
.
∴cos< ![]() >=
>= 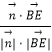 =
= ![]() .
.
∴直线BE与平面PBD所成角的正弦值为 ![]() .
.
【解析】(1)设AC,BD交点为O,连结PO,则PO⊥平面ABCD,于是PO⊥BD,又BD⊥AC,故而BD⊥平面PAC,于是平面EBD⊥平面PAC;(2)以O为原点,以OA,OB,OP为坐标轴建立空间直角坐标系,则 ![]() =(1,0,0)为平面PBD的一个法向量,求出cos<
=(1,0,0)为平面PBD的一个法向量,求出cos< ![]() ,
, ![]() >,则|cos<
>,则|cos< ![]() ,
, ![]() >|即为所求.
>|即为所求.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则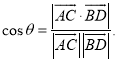 .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.

(Ⅰ)求甲班的平均分;
(Ⅱ)从甲班和乙班成绩90![]() 100的学生中抽取两人,求至少含有甲班一名同学的概率.
100的学生中抽取两人,求至少含有甲班一名同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形![]() ,
, ![]() ,
, ![]() .以
.以![]() 的中点
的中点![]() 为原点建立如图所示的平面直角坐标系
为原点建立如图所示的平面直角坐标系![]() .
.

(1)求以![]() 、
、![]() 为焦点,且过
为焦点,且过![]() 、
、![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 交(1)中椭圆于
交(1)中椭圆于![]() 、
、![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得弦
,使得弦![]() 为直径的圆恰好过原点?若存在,求出直线
为直径的圆恰好过原点?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:曲线C:(m+2)x2+my2=1表示双曲线,命题q:方程y2=(m2﹣1)x表示的曲线是焦点在x轴的负半轴上的抛物线,若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线l与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线l与曲线![]() (为参数)交于A,B两点,点
(为参数)交于A,B两点,点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点。

(1)求直线AF与EC所成角的正弦值;
(2)求PE与平面PDB所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+m|x+a|.
(1)当m=a=﹣1时,求不等式f(x)≥x的解集;
(2)不等式f(x)≥2(0<m<1)恒成立时,实数a的取值范围是{a|a≤﹣3或a≥3},求实数m的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com