
已知函数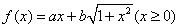 ,且
,且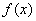 与
与 的函数图象关于直线y=x对称,又
的函数图象关于直线y=x对称,又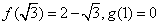 。
。
(1)求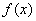 的值域;
的值域;
(2)是否存在实数m,使得命题 满足复合命题“p且q”为真命题?若存在,求出m的取值范围;若不存在,说明理由。
满足复合命题“p且q”为真命题?若存在,求出m的取值范围;若不存在,说明理由。
科目:高中数学 来源: 题型:
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为M(
,且图象上一个点为M( ,-2).
,-2). ]求函数f(x)的值域;
]求函数f(x)的值域; 个单位后得到的函数解析式.
个单位后得到的函数解析式.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西师大附中、临川一中高三(上)8月联考数学试卷(理科)(解析版) 题型:解答题
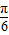 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为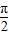 ,且图象上一个点为M(
,且图象上一个点为M(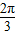 ,-2).
,-2).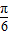 ]求函数f(x)的值域;
]求函数f(x)的值域;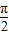 个单位后得到的函数解析式.
个单位后得到的函数解析式.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳市东北育才双语学校高一(上)期中数学试卷(解析版) 题型:解答题
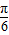 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为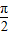 ,且图象上一个点为M(
,且图象上一个点为M(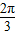 ,-2).
,-2).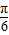 ]求函数f(x)的值域;
]求函数f(x)的值域;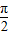 个单位后得到的函数解析式.
个单位后得到的函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com