
【题目】设函数 ![]()
(1)当 ![]() 时,求
时,求 ![]() 的最小值;
的最小值;
(2)若对 ![]() ,都有
,都有 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:当 ![]() 时,
时, ![]() ,
,![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以 ![]() 的最小值为0
的最小值为0
(2)解:因为 ![]() 恒成立,所以
恒成立,所以 ![]() ,
,
而当 ![]() 时,若
时,若 ![]() 则
则 ![]() ;
;
若 ![]() 则
则 ![]() ;
;
若 ![]() 则
则 ![]() .
.
所以当 ![]() 时总有
时总有 ![]() ,因此
,因此 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)代入a值f(x)=x2-2x-2|x-2|+4,分类讨论即可;
(2)利用特殊值先确定一个范围:由f(0)≥0,f(1)≥0,得-2≤a≤1;在对x进行分类讨论.
【考点精析】本题主要考查了函数的单调性和函数的最值及其几何意义的相关知识点,需要掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
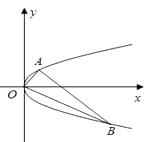
【题目】已知抛物线 ![]() 上的点
上的点 ![]() 到焦点
到焦点 ![]() 的距离为
的距离为 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)设 ![]() ,
, ![]() 是抛物线上分别位于
是抛物线上分别位于 ![]() 轴两侧的两个动点,且
轴两侧的两个动点,且 ![]() (其中
(其中 ![]() 为坐标原点).求证:直线
为坐标原点).求证:直线 ![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定 ![]() ,设函数
,设函数 ![]() 满足:对于任意大于
满足:对于任意大于 ![]() 的正整数
的正整数 ![]() ,
, ![]()
(1)设 ![]() ,则其中一个函数
,则其中一个函数 ![]() 在
在 ![]() 处的函数值为;
处的函数值为;
(2)设 ![]() ,且当
,且当 ![]() 时,
时, ![]() ,则不同的函数
,则不同的函数 ![]() 的个数为。
的个数为。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2﹣3x,函数g(x)的图象在点(1,g(x))处的切线平行于x轴.
(1)求a的值;
(2)求函数g(x)的极小值;
(3)设斜率为k的直线与函数f(x)的图象交于两点A(x1 , y1),B(x2 , y2),(x1<x2),证明: ![]() <k<
<k< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com