【题目】已知函数
，
，
．
(Ⅰ)当
时，求曲线
在
处的切线方程；
(Ⅱ)求
的单调区间；
(Ⅲ)设
，若对于任意
，总存在
，使得
成立，求
的取值范围．
【答案】(Ⅰ)
；(Ⅱ)见解析； (Ⅲ)
.
【解析】
(Ⅰ)求解出点
，再利用导数求出切线斜率，从而得切线方程；(Ⅱ)求导后，分别在
、
和
三个范围中讨论导函数的符号，即可得到原函数的单调性；(Ⅲ)将问题转化为
在
上的值域是
在上的值域的子集，利用导数分别求解出两个函数的值域，从而构造不等式，解出取值范围.
(Ⅰ)当
时，
，所以
所以
所以曲线
在
处的切线方程为
，即
(Ⅱ)
的定义域是
，
令
，得
①当时，
，所以函数的单调增区间是
②当时，
变化如下：
|
|
|
|
|
|
|
| + |
| - | - |
| + |
| ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
所以函数的单调增区间是
，单调减区间是
③当时，变化如下：
|
|
|
|
|
|
|
| + |
| - | - |
| + |
| ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
所以函数的单调增区间是
，单调减区间是
(Ⅲ)因为
，所以
当时，
所以
在
上恒成立，所以在上单调递增
所以在上的最小值是
，最大值是
即当
时，的取值范围为
由(Ⅱ)知，当
时，
，在
上单调递减，在
上单调递增
因为
，所以不合题意
当
时，
，在上单调递减
所以在上的最大值为
，最小值为
所以当时，的取值范围为
“对于任意
，总存在
，使得
成立”等价于
即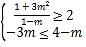
，解得
所以
的取值范围为
科目：高中数学 来源： 题型：
【题目】四色猜想是世界三大数学猜想之一，1976年数学家阿佩尔与哈肯证明，称为四色定理.其内容是：“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域，每一个区域总可以用1，2，3，4四个数字之一标记，而不会使相邻的两个区域得到相同的数字.”如图，网格纸上小正方形的边长为1，粗实线围城的各区域上分别标有数字1，2，3，4的四色地图符合四色定理，区域
和区域
标记的数字丢失.若在该四色地图上随机取一点，则恰好取在标记为1的区域的概率所有可能值中，最大的是______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，圆
的参数方程为
（
为参数），以
为极点，
轴的非负半轴为极轴建立极坐标系，直线
的极坐标方程为
．
（1）求的极坐标方程和直线的直角坐标方程；
（2）射线
与圆的交点为，
，与直线的交点为
，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前n项和为
，且满足
，数列
中，
，对任意正整数
，
.
（1）求数列的通项公式；
（2）是否存在实数
，使得数列
是等比数列？若存在，请求出实数及公比q的值，若不存在，请说明理由；
（3）求数列前n项和
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中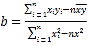
，
.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑，PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上，则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
