Question

已知等差数列{a_n}的首项a₁=1,公差d>0，且第2项，第5项，第14项分别是等比数列{b_n}的第2项，第3项，第4项．

（1）求数列{a_n}与{b_n}的通项公式；

 (2)求数列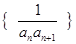的前n项和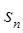

（3）设数列{c_n}对任意自然数n，均有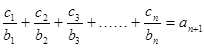，求c₁+c₂+c₃+……+c₂₀₀₆值．

 

Answer 1

【答案】

（1）a_n=2n-1,b_n=3^n-1.（2）见解析

（3）当n=1时，c₁=3 当n≥2时， ，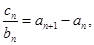

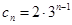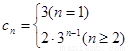
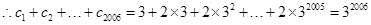
【解析】

试题分析：（1）利用等差数列的通项公式将第二项，第五项，第十四项用{a_n}的首项与公差表示，再据此三项成等比数列，列出方程，求出公差，利用等差数列及等比数列的通项公式求出数列{a_n}与{b_n}的通项公式．

（2）根据数列的通项公式通过裂项求解数列的和

（3）当n≥2时，根据a_n+1-a_n，求出数列{c_n}通项公式，但当n=1时，不符合上式，因此数列{c_n}是分段数列；然后根据通项公式即可求出结果

解：（1）由题意得（a₁+d）(a₁+13d)=(a₁+4d)²(d>0)  解得d=2,∴a_n=2n-1,b_n=3^n-1.

（3）当n=1时，c₁=3 当n≥2时， ，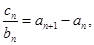

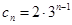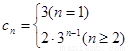
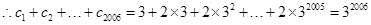
考点：本试题主要考查了利用基本量表示等差数列、等比数列的通项，叠加求解数列的通项．

点评：解决该试题的关键是对于等差数列，等比数列基本关系式的求解和运用。