
课本中只针对椭圆的标准方程形式来讨论了相应的椭圆所具有的性质,对于其方程不是标准方程(或经过变形也不能转化为标准方程的形式)的椭圆是否也具有相似的性质呢?
科目:高中数学 来源: 题型:
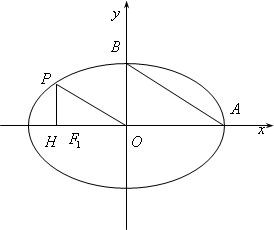 已知在椭圆C:
已知在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
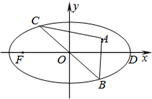 已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为F(-
已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为F(-| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com