
【题目】已知点P是长轴长为 ![]() 的椭圆Q:
的椭圆Q: ![]() 上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为
上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为 ![]() .
.
(1)求椭圆Q的方程;
(2)设过左焦点F1且不与坐标轴垂直的直线l交椭圆于C,D两点,线段CD的垂直平分线与x轴交于点G,点G横坐标的取值范围是 ![]() ,求|CD|的最小值.
,求|CD|的最小值.
【答案】
(1)解:∵椭圆Q的长轴长为 ![]() ,∴
,∴ ![]() .
.
设P(x0,y0),
∵直线PA与OM的斜率之积恒为 ![]() ,∴
,∴ 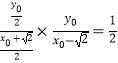 ,
,
∴ ![]() ,∴b=1,
,∴b=1,
故椭圆的方程为 ![]()
(2)解:设直线l方程为y=k(x+1)(k≠0),代入 ![]() 有(1+2k2)x2+4k2x+2k2﹣2=0,
有(1+2k2)x2+4k2x+2k2﹣2=0,
设A(x1,y1),B(x2,y2),AB中点N(x0,y0),
∴ ![]() .
.
∴ ![]()
∴CD的垂直平分线方程为 ![]() ,
,
令y=0,得 ![]()
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .
. ![]() =
= ![]() ,
, ![]()
【解析】(1)利用椭圆Q的长轴长为 ![]() ,求出
,求出 ![]() .设P(x0 , y0),通过直线PA与OM的斜率之积恒为
.设P(x0 , y0),通过直线PA与OM的斜率之积恒为 ![]() ,化简求出b,即可得到椭圆方程.(2)设直线l方程为y=k(x+1)(k≠0),代入
,化简求出b,即可得到椭圆方程.(2)设直线l方程为y=k(x+1)(k≠0),代入 ![]() 有(1+2k2)x2+4k2x+2k2﹣2=0,设A(x1 , y1),B(x2 , y2),AB中点N(x0 , y0),利用韦达定理求出CD的垂直平分线方程,推出
有(1+2k2)x2+4k2x+2k2﹣2=0,设A(x1 , y1),B(x2 , y2),AB中点N(x0 , y0),利用韦达定理求出CD的垂直平分线方程,推出 ![]() ,利用弦长公式化简,推出|CD|的最小值.
,利用弦长公式化简,推出|CD|的最小值.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据中点坐标公式求出![]() 中点
中点![]() 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得![]() 的斜率,利用点斜式可求
的斜率,利用点斜式可求![]() 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出![]() 的斜率,从而求出
的斜率,从而求出![]() 边上的高所在直线的斜率为
边上的高所在直线的斜率为![]() ,利用点斜式可求
,利用点斜式可求![]() 边上的高所在直线的方程.
边上的高所在直线的方程.
试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=![]() =8,
=8,
所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=![]() =1,
=1,
所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生1 000名,经调查,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学,如果以身高达165 cm作为达标的标准,对抽取的100名学生,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
(1)完成上表;
(2)能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com