练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】刘徽是我国古代伟大的数学家，他的杰作《九章算术注》和《海岛算经》是我国最宝贵的数学遗产刘徽是世界上最早提出十进小数概念的人，他正确地提出了正负数的概念及其加减运算的规则．提出了“割圆术”，并用“割圆术”求出圆周率π为3.14．刘徽在割圆术中提出的“割之弥细，所失弥少，割之又割以至于不可割，则与圆合体而无所失矣”被视为中国古代极限观念的佳作．其中“割圆术”的第一步是求圆的内接正六边形的面积，第二步是求圆的内接正十二边形的面积，依此类推．若在圆内随机取一点，则该点取自该圆内接正十二边形的概率为（　　）

    A.B.C.D.

    【答案】C

    【解析】

    设圆的半径为1，分别求出圆的面积及圆内接正十二边形的面积，由测度比是面积比得答案．

    解：设圆的半径为1，圆内接正十二边形的一边所对的圆心角为

    则圆内接正十二边形的面积为：

    圆的面积为，

    由测度比为面积比可得：在圆内随机取一点，则此点在圆的某一个内接正十二边形内的概率是．

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

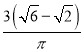
    科目：高中数学 来源： 题型：

    【题目】设椭圆的右顶点为A，上顶点为B．已知椭圆的离心率为，．

    （1）求椭圆的方程；

    （2）设直线与椭圆交于，两点，与直线交于点M，且点P，M均在第四象限．若的面积是面积的2倍，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求曲线在点处的切线方程；

    （2）求函数的零点和极值；

    （3）若对任意，都有成立，求实数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（多选题）下列说法正确的是（ ）

    A.在回归直线方程中，当解释变量每增加1个单位时，预报变量平均减少2.3个单位

    B.两个具有线性相关关系的变量，当相关指数的值越接近于0，则这两个变量的相关性就越强

    C.若两个变量的相关指数，则说明预报变量的差异有88%是由解释变量引起的

    D.在回归直线方程中，相对于样本点的残差为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点F1为椭圆的左焦点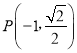，在椭圆上，PF1⊥x轴．

    （1）求椭圆的方程：

    （2）已知直线l与椭圆交于A，B两点，且坐标原点O到直线l的距离为的大小是否为定值？若是，求出该定值：若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的最大值为，且曲线在x＝0处的切线与直线平行（其中e为自然对数的底数）．

    （1）求实数a，b的值；

    （2）如果，且，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位年会进行抽奖活动，在抽奖箱里装有张印有“一等奖”的卡片， 张印

    有“二等奖”的卡片， 3张印有“新年快乐”的卡片，抽中“一等奖”获奖元， 抽中“二等奖”获奖元，抽中“新年快乐”无奖金.

    （1）单位员工小张参加抽奖活动，每次随机抽取一张卡片，抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记表示“小张恰好抽奖次停止活动”，求的值；

    （2）若单位员工小王参加抽奖活动，一次随机抽取张卡片.

    ①记表示“小王参加抽奖活动中奖”，求的值；

    ②设表示“小王参加抽奖活动所获奖金数（单位：元）”，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在上存在单调递增区间，求实数的取值范围；

    （2）设，若，恒有成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，准线为，为过焦点且垂直于轴的抛物线的弦，已知以为直径的圆经过点.

    （1）求的值及该圆的方程；

    （2）设为上任意一点，过点作的切线，切点为，证明：.

    查看答案和解析>>

    同步练习册答案