Question

【题目】已知二次函数满足①对于任意，都有；②；③的图像与轴的两个交点之间的距离为4.

（1）求的解析式；

（2）记

①若为单调函数，求的取值范围；

②记的最小值为，讨论函数零点的个数.

Answer 1

【答案】（1）（2）①或②详见解析

【解析】

（1）根据条件可知二次函数对称轴，的图像与轴的两个交点之间的距离为4可求出交点，利用交点式求函数解析式（2）①写出二次函数，根据对称轴与区间关系可求出的取值范围②分类讨论求出函数的最小值，换元后作出函数图象，再利用数形结合研究函数的零点，注意分类讨论思想在解题中的应用.

（1）因为二次函数中，

所以对称轴，

又的图像与轴的两个交点之间的距离为4，

所以与轴交点为

设，

又，

所以

即.

（2）① ,

对称轴为，

因为为单调函数，

所以或

解得或.

故的取值范围是或.

②,

对称轴为，

当，即时，，

当，即时，，

当，即时，

综上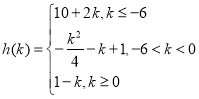

函数零点即为方程的根，

令，即的根，

作出的简图如图所示：

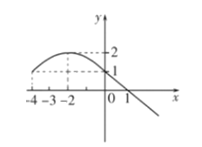
（i）当时，，或，

解得或，有3个零点.

（ii）当时，有唯一解，解得，有2个零点.

（iii）当时，有两个不同的解，

解得或，有4个零点.

（iv）当时，，，解得，有2个零点.

（v）当时，无解，无零点.

综上：当时，无零点；

当时，4个零点；

当时，有3个零点；

当或时，有2个零点.