
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求![]() 的值域;
的值域;
(3)求![]() 的递增区间
的递增区间
(4)求![]() 的对称轴;
的对称轴;
(5)求![]() 的对称中心;
的对称中心;
(6)![]() 的三边a,b,c满足
的三边a,b,c满足![]() ,且b所对的角为x,求x的取值范围及函数
,且b所对的角为x,求x的取值范围及函数![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)直线
;(4)直线![]() ;(5)对称中心
;(5)对称中心![]() ;(6)
;(6)![]() ,值域为
,值域为![]()
【解析】
对于(1)——(5)根据题意,对![]() 进行三角恒等变换,化简成
进行三角恒等变换,化简成![]() ,然后即可求出
,然后即可求出![]() 的各种性质;
的各种性质;
对于(6),通过余弦定理和基本不等式的性质,可求得![]() 的取值范围,进而可求出
的取值范围,进而可求出![]() 的值域;
的值域;
根据题意,![]() ,进行化简,
,进行化简,
![]()
![]()
![]() ,据此可得,
,据此可得,
(1)![]() 的最小正周期为
的最小正周期为![]() ;
;
答案:![]()
(2)![]() 的值域为
的值域为![]() ;
;
答案:![]()
(3)![]() 的递增区间为
的递增区间为![]() ,化简得
,化简得
![]() ,所以,
,所以,
![]() 的递增区间为
的递增区间为![]()
答案:![]()
(4)对于![]() ,令
,令![]() ,化简得
,化简得![]() ,即
,即![]() 的对称轴为直线
的对称轴为直线![]()
答案:直线![]()
(5)对于![]() ,令
,令![]() ,化简得,
,化简得,![]() ,所以,对称中心为
,所以,对称中心为![]() ;
;
答案:对称中心![]()
(6) 对于![]() 的三边a,b,c满足
的三边a,b,c满足![]() ①,且b所对的角为x,
①,且b所对的角为x,![]() ,
,
根据余弦定理得,![]() ②,
②,
由①和②得![]() ,
,
即![]() ,所以,
,所以,![]() ,对于
,对于![]() ,
,
可知,![]() ,则
,则![]() ;
;
答案:![]() ,值域为
,值域为![]()


科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() ,存在实数
,存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.给出下列命题:
性质”.给出下列命题:
①函数![]() 具有“
具有“![]() 性质”;
性质”;
②若奇函数![]() 具有“
具有“![]() 性质”,且
性质”,且![]() ,则
,则![]() ;
;
③若函数![]() 具有“
具有“![]() 性质”,图象关于点
性质”,图象关于点![]() 成中心对称,且在
成中心对称,且在![]() 上单调递减,则
上单调递减,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
④若不恒为零的函数![]() 同时具有“
同时具有“![]() 性质”和“
性质”和“![]() 性质”,且函数
性质”,且函数![]() 对
对![]() ,都有
,都有![]()
![]() 成立,则函数
成立,则函数![]() 是周期函数.
是周期函数.
其中正确的是__________(写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+1+|3-x|,x≥-1.
(1)求不等式f(x)≤6的解集;
(2)若f(x)的最小值为n,正数a,b满足2nab=a+2b,求2a+b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数
![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的
个单位后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市11月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月12日中的某一天到达该市,并停留3天.
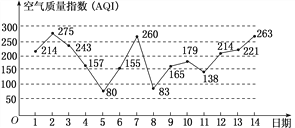
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气重度污染的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下间题:“今有甲、乙、丙、丁、戊五人分五饯,令上二人所得与下三人等,且五人所得钱按顺序等次差,问各得几何?”其意思为“甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱(钱:古代一种重量单位)?”这个问题中丙所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C. 1钱 D.
钱 C. 1钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数.若存在,求出定点
的斜率之积为常数.若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com