⑤
分析:命题①利用函数的对称变换和平移变换进行分析;
命题②利用复合函数,先求出指数的范围,再求复合函数的值域;
命题③先利用复合函数的单调性求出a的范围,然后利用函数是偶函数把f(-2)转化为f(2)比较大小;
命题④是分段函数,保证函数在每一段上都是减函数,且第一段的最小值要大于等于第二段的最大值;
命题⑤通过画图分析知一个根小于1,一个根大于1,把两个根代入方程后取绝对值相加,整理后可得0<x
1x
2<1.
解答:由f(-x+2)=f[-(x-2)],所以函数y=f(-x+2)的图象是把函数y=f(-x)的图象向右平移2个单位得到的,
y=f(x-2)的图象是把y=f(x)的图象向右平移2个单位得到的,而y=f(x)与y=f(-x)的图象关于y轴轴对称,
所以,函数y=f(-x+2)与y=f(x-2)的图象关于直线x=2对称.所以,命题①错误;
令x
2+2x=t,则函数函数
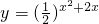
化为
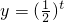
,又t=x
2+2x=(x+1)
2-1≥-1,
0<
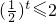
,即函数
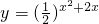
的值域是(0,2].所以命题②错误;
函数f(x)=log
a|x|(a>0,a≠1)在(0,+∞)上单调递增,因为t=|x|在(0,+∞)上单调递增,所以,
函数y=log
at也在(0,+∞)上单调递增,则a>1,a+1>2.又因为函数f(x)=log
2|x|是偶函数,
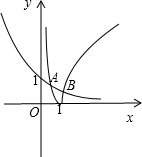
所以f(-2)=f(2),则f(-2)=f(2)<f(a+1).所以,命题③错误;
由f(x)=
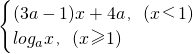
是(-∞,+∞)上的减函数,则
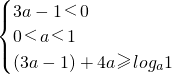
,
解得:
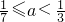
.所以,命题④错误;
令
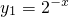
,y
2=|lgx|,
在平面直角坐标系中作出这两个函数的图象如图,
不妨设A点的横坐标为x
1,B点的横坐标为x
2,则x
1<1<x
2,
由

,得
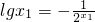
,
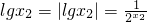
,得:
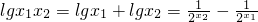
=
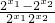
<0.
所以,0<x
1x
2<1.所以,命题⑤正确.
故答案为⑤.
点评:本题考查了命题的真假判断与应用,综合考查了函数图象的平移和对称变换,复合函数的值域以及函数的单调性等特性,考查了方程的根和函数零点的关系,此题是中档题.

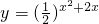 的值域是[2,+∞);
的值域是[2,+∞);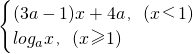 是(-∞,+∞)上的减函数,则a的取值范围是(0,
是(-∞,+∞)上的减函数,则a的取值范围是(0, );
);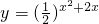 化为
化为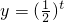 ,又t=x2+2x=(x+1)2-1≥-1,
,又t=x2+2x=(x+1)2-1≥-1,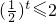 ,即函数
,即函数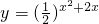 的值域是(0,2].所以命题②错误;
的值域是(0,2].所以命题②错误;
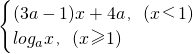 是(-∞,+∞)上的减函数,则
是(-∞,+∞)上的减函数,则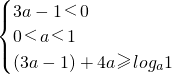 ,
,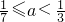 .所以,命题④错误;
.所以,命题④错误;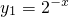 ,y2=|lgx|,
,y2=|lgx|, ,得
,得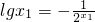 ,
,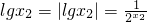 ,得:
,得: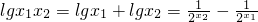 =
=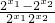 <0.
<0.

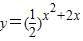 的值域是[2,+∞);
的值域是[2,+∞);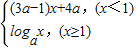 是(-∞,+∞)上的减函数,则a的取值范围是(0,
是(-∞,+∞)上的减函数,则a的取值范围是(0, );
);