
(本题12分)已知P: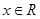 且
且 ,已知Q:
,已知Q: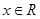 且
且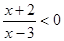 .
.
(Ⅰ)在区间(-4,4)上任取一个实数x,求命题“P且Q”为真的概率;
(Ⅱ)设在数对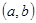 中,
中,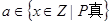 ,
,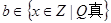 ,求“事件
,求“事件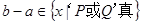 ”发生的概率.
”发生的概率.
(Ⅰ)在区间(-4,4)上任取一个实数x,命题“P且Q”为真的概率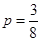 .
.
(Ⅱ)事件“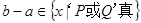 ”发生的概率
”发生的概率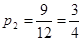 .
.
【解析】
试题分析:(Ⅰ)P真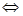
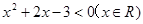
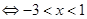 ;
;
Q真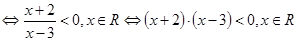
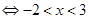 ;
;
“P且Q”真
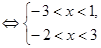
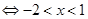 .
.
区间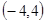 的长度为8,区间
的长度为8,区间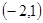 的长度为3,
的长度为3,
故在区间(-4,4)上任取一个实数x,命题“P且Q”为真的概率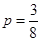 . …………6分
. …………6分
(Ⅱ)在(Ⅰ)的基础上易知, 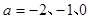 ,
,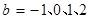 ,则基本事件
,则基本事件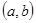 共有12个:(-2,-1),(-2,0),(-2,1),(-2,2),(-1,-1),(-1,0),(-1,1),(-1,2),(0, -1),(0,0),(0,1),(0,2).
共有12个:(-2,-1),(-2,0),(-2,1),(-2,2),(-1,-1),(-1,0),(-1,1),(-1,2),(0, -1),(0,0),(0,1),(0,2).
“P或Q”真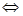 P真或Q真
P真或Q真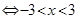 ,符合
,符合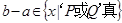 的基本事件为:(-2,-1),(-2,0),(-1,-1),(-1,0),(-11),(0, -1),(0,0),(0,1),(0,2),共9个.
的基本事件为:(-2,-1),(-2,0),(-1,-1),(-1,0),(-11),(0, -1),(0,0),(0,1),(0,2),共9个.
故事件“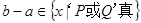 ”发生的概率
”发生的概率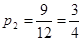 . …………………………12分
. …………………………12分
考点:本题主要考查命题,简易逻辑连接词,古典概型概率的计算。
点评:综合题,判断命题的真假,往往涉及知识方法较多,对复合命题,真值表的利用是常考点。古典概型概率的计算,公式明确,关键是计算基本事件数要准确,可借助于“树图法”“坐标法”。


科目:高中数学 来源:2012届甘肃省兰州一中高三上学期期中考试理科数学试卷 题型:解答题
(本题12分)已知函数 对任意实数p、q都满足
对任意实数p、q都满足
 .
.
(Ⅰ)当
 时,求
时,求 的表达式;
的表达式;
(Ⅱ)设 求
求 ;
;
(Ⅲ)设 求证:
求证: .
.
查看答案和解析>>
科目:高中数学 来源:2011年广东省揭阳市高二上学期期末检测数学理卷 题型:解答题
本题12分)已知 且
且 ,命题P:函数
,命题P:函数 在区间
在区间 上为减函数;命题Q:曲线
上为减函数;命题Q:曲线 与
与 轴相交于不同的两点.若“
轴相交于不同的两点.若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二第一学期期末考试文科数学 题型:解答题
(本题12分)已知函数 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源:2013届四川省巴中市四县中高二上学期期末考试理科数学 题型:解答题
((本题12分)已知P与平面上两定点A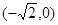 ,B
,B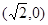 连线的斜率的积为定值
连线的斜率的积为定值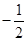 ,
,
(Ⅰ)试求动点P的轨迹方程C;
(Ⅱ)设直线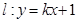 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|=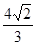 时,求直线
时,求直线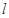 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com