
已知椭圆E: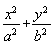 =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=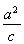 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且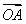 ⊥
⊥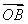 ,求出该圆的方程.
,求出该圆的方程.
(1)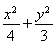 =1(2)x2+y2=
=1(2)x2+y2=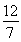
【解析】(1)由题知2|F1F2|=|MF1|+|MF2|,
即2×2c=2a,得a=2c.
又由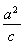 -c=3,解得c=1,a=2,b=
-c=3,解得c=1,a=2,b=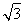 .
.
∴椭圆E的方程为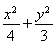 =1.
=1.
(2)假设以原点为圆心,r为半径的圆满足条件.
(ⅰ)若圆的切线的斜率存在,并设其方程为y=kx+m,则r=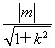 ,r2=
,r2=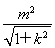 ,①
,①
由 消去y,整理得(3+4k2)x2+8kmx+4(m2-3)=0,设A(x1,y1),B(x2,y2),有
消去y,整理得(3+4k2)x2+8kmx+4(m2-3)=0,设A(x1,y1),B(x2,y2),有
又∵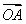 ⊥
⊥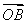 ,∴x1x2+y1y2=0,
,∴x1x2+y1y2=0,
即4(1+k2)(m2-3)-8k2m2+3m2+4k2m2=0,化简得m2=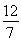 (k2+1),②
(k2+1),②
由①②求得r2=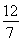 .
.
所求圆的方程为x2+y2=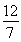 .
.
(ⅱ)若AB的斜率不存在,设A(x1,y1),则B(x1,-y1),∵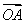 ⊥
⊥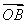 ,∴
,∴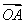 ·
·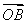 =0,有
=0,有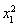 -
-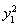 =0,
=0, =
=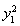 ,代入
,代入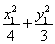 =1,得
=1,得 =
=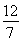 .此时仍有r2=|
.此时仍有r2=|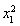 |=
|=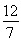 .
.
综上,总存在以原点为圆心的圆x2+y2=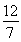 满足题设条件
满足题设条件


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:选择题
已知球的半径为5,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2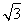 ,若其中一个圆的半径为4,则另一个圆的半径为( )
,若其中一个圆的半径为4,则另一个圆的半径为( )
A.3 B.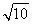 C.
C.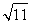 D.2
D.2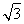
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:填空题
高三(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论是:有________的把握认为“学生性别与支持该活动有关系”( )
附:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B.1% C.99% D.99.9%
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:填空题
已知双曲线x2-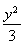 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则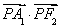 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点A、B到y轴的距离分别为m,n,则m+n+2的最小值为( )
A.4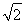 B.6
B.6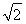 C.4 D.6
C.4 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com