Question

【题目】如图，正三棱柱中为的中点。

（1）求证：；

（2）若点为四边形内部及其边界上的点，且三棱锥的体积为三棱柱体积的，试在图中画出点的轨迹，并说明理由。

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1）取的中点，连接，由为正三角形可得，又，从而可得平面，所以．在正方形中可证得，然后根据线面垂直的判定定理得到平面，故得．（2）取中点，连接，则线段为点的运动轨迹，然后根据线面平行的性质可证得结论成立．

解法一：（1）证明：取的中点，连接，

∵平面，平面，

∴．

∵为正三角形，为的中点，

∴，

又∵平面，，

∴平面，

又平面，

∴

在正方形中，可得，

∴，

又∵，

∴，故，

又，平面，

∴平面，

∵平面，

∴．

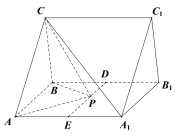
（2）取中点，连接，则线段为点的运动轨迹．理由如下：

∵，平面，平面，

∴平面，

∴到平面的距离为．

∴．

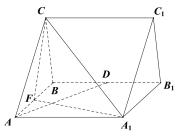
故线段为点的运动轨迹．

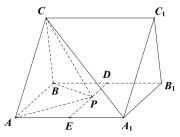
解法二：（1）证明：取的中点，连接，

∵为正三角形，为的中点，

∴．

∵在正三棱柱中，平面平面，平面平面，平面，

∴平面，

∴．

在正方形中，因为，

∴，

又，

∴，

∴，

又，平面，

∴平面，

又，

∴．

（2）取中点，连接，则线段为点的运动轨迹．理由如下：

设三棱锥的高为，

依题意得，

∴．

∵分别为中点，

∴，

又平面，平面，

∴平面，

∴点到平面的距离为．

故线段为点的运动轨迹．