
【题目】下列命题中正确的命题有( )个
(1)如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
(2)如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
(3)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么
,那么![]() 平面
平面![]()
(4)如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】(1)结合实物:教室的门面与地面垂直,门面的上棱对应的直线就与地面平行,故此命题成立;(2)假若平面![]() 内存在直线垂直于平面
内存在直线垂直于平面![]() ,根据面面垂直的判定定理可知两平面垂直,故此命题成立;(3)结合面面垂直的性质可以分别在
,根据面面垂直的判定定理可知两平面垂直,故此命题成立;(3)结合面面垂直的性质可以分别在![]() 内作异于
内作异于![]() 的直线垂直于交线,再由线面垂直的性质定理可知所作的垂线平行,进而得到线面平行再由线面平行的性质可知所作的直线与
的直线垂直于交线,再由线面垂直的性质定理可知所作的垂线平行,进而得到线面平行再由线面平行的性质可知所作的直线与![]() 平行,又
平行,又![]() 两条平行线中的一条垂直于平面那么另一条也垂直于平面,故命题成立;(4)举反例:教室内侧墙面与地面垂直,而侧墙面内有很多直线是不垂直与地面的,故此命题错误,
两条平行线中的一条垂直于平面那么另一条也垂直于平面,故命题成立;(4)举反例:教室内侧墙面与地面垂直,而侧墙面内有很多直线是不垂直与地面的,故此命题错误,![]() 正确的命题有
正确的命题有![]() 个,故选C.
个,故选C.
【方法点晴】本题主要考查线面平行的判定与性质、面面垂直的性质及线面垂直的判定,属于难题.空间直线、平面平行或垂直等位置关系命题的真假判断,常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.


科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,设直线
,设直线![]() 的斜率是
的斜率是![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的标准方程.
(Ⅱ)若直线![]() 在
在![]() 轴上的截距是
轴上的截距是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年下半年起六安市区商品房价不断上涨,为了调查研究六安城区居民对六安商品房价格承受情况,寒假期间小明在六安市区不同小区分别对50户居民家庭进行了抽查,并统计出这50户家庭对商品房的承受价格(单位:元/平方),将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组(单位:元/平方),并作出频率分布直方图如图:
五组(单位:元/平方),并作出频率分布直方图如图:
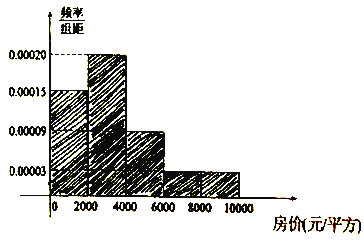
(Ⅰ)试根据频率分布直方图估计出这50户家庭对商品房的承受价格平均值(单位:元/平方);
(Ⅱ)为了作进一步调查研究,小明准备从承受能力超过4000元/平方的居民中随机抽出2户进行再调查,设抽出承受能力超过8000元/平方的居民为![]() 户,求
户,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,a,b,c分别是△ABC三个内角A,B,C的对边,下列四个命题:
①若tanA+tanB+tanC>0,则△ABC是锐角三角形
②若acoA=bcosB,则△ABC是等腰三角形
③若bcosC+ccosB=b,则△ABC是等腰三角形
④若 ![]() =
= ![]() ,则△ABC是等边三角形
,则△ABC是等边三角形
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A′B′C′D′. 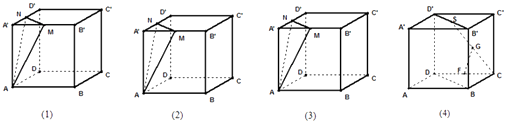
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com