(Ⅰ)解:求导函数,可得
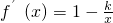
,因为x=1是函数f(x)的一个极值点,f′(1)=0,∴k=1,…(2分)
所以
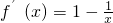
令f′(x)>0,可得x∈(1,+∞)∪(-∞,0),∵x>0,∴x∈(1,+∞)
令f′(x)<0,可得x∈(0,1)…(3分)
故函数F(x)的单调递增区间是(1,+∞),单调递减区间是(0,1).…(4分)
(Ⅱ)解:因为函数g(x)=xf(x)在区间(1,2)上是增函数,则g′(x)=2x-k(1+lnx)≥0对x∈(1,2)恒成立,即

对x∈(1,2)恒成立 …(5分)
令
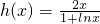
,则知

对x∈(1,2)恒成立.…(6分)
所以
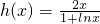
在x∈(1,2)单调递增,h
min(x)>h(1)=2..….…(7分)
所以k≤2.(8分)
(Ⅲ)证明:F(x)=
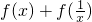
=

,F(1)F(2)F(3)…F(2n)=(
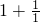
)(
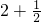
)…(
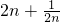
)
因为(
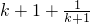
)(
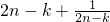
)=
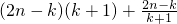
+
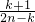
+
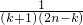
>(2n-k)(k+1)+2=2n+2+2nk-k
2-k=2n+2+k(2n-k-1)>2n+2.…(10分)
(k=0,1,2,3…n-1)
所以(
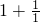
)(
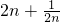
)>2n+2,(
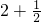
)(
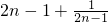
)>2n+2,…,(
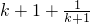
)(
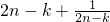
)>2n+2,(

)(
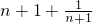
)>2n+2.…(11分)
相乘,得:F(1)F(2)F(3)…F(2n)
=(
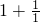
)(
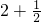
)…(
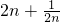
)>(2n+2)
n=2
n(n+1)
n.…(12分)
分析:(Ⅰ)求导函数,根据x=1是函数f(x)的一个极值点,可求k的值,令f′(x)>0,可得函数F(x)的单调递增区间,令f′(x)<0,可得单调递减区间;
(Ⅱ)根据函数g(x)=xf(x)在区间(1,2)上是增函数,可得g′(x)=2x-k(1+lnx)≥0对x∈(1,2)恒成立,即

对x∈(1,2)恒成立,令
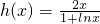
,求出最小值,即可求得k的取值范围;
(Ⅲ)先证明(
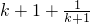
)(
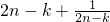
)>2n+2,再利用叠乘即可得到结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明,解题的关键是分离参数,确定函数的最值.

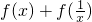 ,求证:F(1)F(2)F(3)…F(2n)>2n(n+1)n(n∈N*).
,求证:F(1)F(2)F(3)…F(2n)>2n(n+1)n(n∈N*).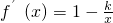 ,因为x=1是函数f(x)的一个极值点,f′(1)=0,∴k=1,…(2分)
,因为x=1是函数f(x)的一个极值点,f′(1)=0,∴k=1,…(2分)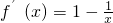
 对x∈(1,2)恒成立 …(5分)
对x∈(1,2)恒成立 …(5分)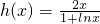 ,则知
,则知 对x∈(1,2)恒成立.…(6分)
对x∈(1,2)恒成立.…(6分)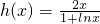 在x∈(1,2)单调递增,hmin(x)>h(1)=2..….…(7分)
在x∈(1,2)单调递增,hmin(x)>h(1)=2..….…(7分)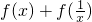 =
= ,F(1)F(2)F(3)…F(2n)=(
,F(1)F(2)F(3)…F(2n)=(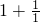 )(
)(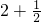 )…(
)…(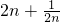 )
)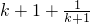 )(
)(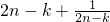 )=
)=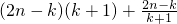 +
+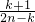 +
+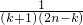 >(2n-k)(k+1)+2=2n+2+2nk-k2-k=2n+2+k(2n-k-1)>2n+2.…(10分)
>(2n-k)(k+1)+2=2n+2+2nk-k2-k=2n+2+k(2n-k-1)>2n+2.…(10分)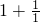 )(
)(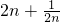 )>2n+2,(
)>2n+2,(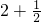 )(
)(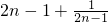 )>2n+2,…,(
)>2n+2,…,(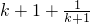 )(
)(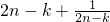 )>2n+2,(
)>2n+2,( )(
)(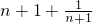 )>2n+2.…(11分)
)>2n+2.…(11分)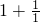 )(
)(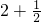 )…(
)…(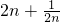 )>(2n+2)n=2n(n+1)n.…(12分)
)>(2n+2)n=2n(n+1)n.…(12分) 对x∈(1,2)恒成立,令
对x∈(1,2)恒成立,令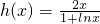 ,求出最小值,即可求得k的取值范围;
,求出最小值,即可求得k的取值范围;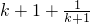 )(
)(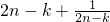 )>2n+2,再利用叠乘即可得到结论.
)>2n+2,再利用叠乘即可得到结论.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<