
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=![]() (a2+c2﹣b2).
(a2+c2﹣b2).
(1)求角B的大小;
(2)若边b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
【答案】(1)B=60°(2)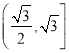
【解析】
(1)由三角形的面积公式,余弦定理化简已知等式可求tanB的值,结合B的范围可求B的值.
(2)由正弦定理,三角函数恒等变换的应用可求a+c![]() sin(A
sin(A![]() ),由题意可求范围A
),由题意可求范围A![]() ∈(
∈(![]() ,
,![]() ),根据正弦函数的图象和性质即可求解.
),根据正弦函数的图象和性质即可求解.
(1)在△ABC中,∵S![]() (a2+c2﹣b2)
(a2+c2﹣b2)![]() acsinB,cosB
acsinB,cosB![]() .
.
∴tanB![]() ,
,
∵B∈(0,π),
∴B![]() .
.
(2)∵B![]() ,b
,b![]() ,
,
∴由正弦定理可得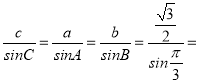 1,可得:a=sinA,c=sinC,
1,可得:a=sinA,c=sinC,
∴a+c=sinA+sinC=sinA+sin(![]() A)=sinA
A)=sinA![]() cosA
cosA![]() sinA
sinA![]() sin(A
sin(A![]() ),
),
∵A∈(0,![]() ),A
),A![]() ∈(
∈(![]() ,
,![]() ),
),
∴sin(A![]() )∈(
)∈(![]() ,1],
,1],
∴a+c![]() sin(A
sin(A![]() )∈(
)∈(![]() ,
,![]() ].
].


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 是平面α内的一组基向量,O为α内的定点,对于α内任意一点P,当
是平面α内的一组基向量,O为α内的定点,对于α内任意一点P,当![]() =x
=x![]() +y
+y![]() 时,则称有序实数对(x,y)为点P的广义坐标.若点A、B的广义坐标分别为(x1,y1)(x2,y2),关于下列命题正确的是:()
时,则称有序实数对(x,y)为点P的广义坐标.若点A、B的广义坐标分别为(x1,y1)(x2,y2),关于下列命题正确的是:()
A.线段A、B的中点的广义坐标为(![]() );
);
B.A、B两点间的距离为![]() ;
;
C.向量![]() 平行于向量
平行于向量![]() 的充要条件是x1y2=x2y1;
的充要条件是x1y2=x2y1;
D.向量![]() 垂直于
垂直于![]() 的充要条件是x1y2+x2y1=0
的充要条件是x1y2+x2y1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的![]() 名市民中,随机抽取
名市民中,随机抽取![]() 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:

分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)求频数分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,从年龄在
名市民中,从年龄在![]() 、
、![]() 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取![]() 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…, ![]() ,…,即当
,…,即当 ![]() <n≤
<n≤ ![]() (k∈N*)时,
(k∈N*)时, ![]() .记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
.记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
(1)求P11中元素个数;
(2)求集合P2000中元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等腰直角三角形ABC中,AB=AC=4,点P是边AB边上异于AB的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的重心,则AP等于( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《厉害了,我的国》这部电影记录:到2017年底,我国高铁营运里程达2.5万公里,位居世界第一位,超过第二名至第十名的总和,约占世界高铁总量的三分之二.如图是我国2009年至2017年高铁营运里程(单位:万公里)的折线图.

根据这9年的高铁营运里程,甲、乙两位同学分别选择了![]() 与时间变量
与时间变量![]() 的两个回归模型①:
的两个回归模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精确到0.01);
(精确到0.01);
(2)乙求得模型②的回归方程为![]() ,你认为哪个模型的拟合效果更好?并说明理由.
,你认为哪个模型的拟合效果更好?并说明理由.
附:参考公式: ,
,![]() ,
,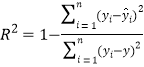 .
.
参考数据:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解当下高二男生的身高状况,某地区对高二年级男生的身高(单位: ![]() )进行了抽样调查,得到的频率分布直方图如图所示.已知身高在
)进行了抽样调查,得到的频率分布直方图如图所示.已知身高在![]() 之间的男生人数比身高在
之间的男生人数比身高在![]() 之间的人数少1人.
之间的人数少1人.
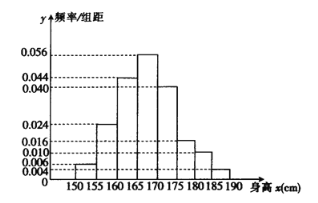
(1)若身高在![]() 以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
(2)从所抽取的样本中身高在![]() 和
和![]() 的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185
的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1 , V2 , V3 , V4 , 上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( ) 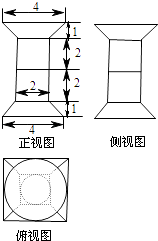
A.V1<V2<V4<V3
B.V1<V3<V2<V4
C.V2<V1<V3<V4
D.V2<V3<V1<V4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ![]() ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O= ![]() .
. 
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com