
【题目】已知向量 ![]() =(sinx,1),
=(sinx,1), ![]() =
= ![]() ,函数f(x)=
,函数f(x)= ![]() 的最大值为6.
的最大值为6.
(1)求A;
(2)将函数f(x)的图象向左平移 ![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0, ![]() ]上的值域.
]上的值域.
【答案】
(1)解:f(x)= ![]() =
= ![]() Asinxcosx+
Asinxcosx+ ![]() cos2x
cos2x
=A( ![]() sin2x+
sin2x+ ![]() cos2x)
cos2x)
=Asin(2x+ ![]() ),
),
∵函数f(x)= ![]() 的最大值为6,
的最大值为6,
∴A=6
(2)解:f(x)=6sin(2x+ ![]() )
) ![]() y=6sin(2(x+
y=6sin(2(x+ ![]() )+
)+ ![]() )=6sin(2x+
)=6sin(2x+ ![]() )
)
![]() y=6sin(4x+
y=6sin(4x+ ![]() ),
),
则g(x)=6sin(4x+ ![]() ),
),
∵0≤x≤ ![]() ,
,
∴0≤4x≤ ![]() ,
,
∴ ![]() ≤4x+
≤4x+ ![]() ≤
≤ ![]() ,
,
∴- ![]() ≤sin(4x+
≤sin(4x+ ![]() )≤1,
)≤1,
∴﹣3≤6sin(4x+ ![]() )≤6,
)≤6,
即g(x)在[0, ![]() ]上的值域为[﹣3,6]
]上的值域为[﹣3,6]
【解析】(1)化f(x)= ![]() =
= ![]() Asinxcosx+
Asinxcosx+ ![]() cos2x=A(
cos2x=A( ![]() sin2x+
sin2x+ ![]() cos2x)=Asin(2x+
cos2x)=Asin(2x+ ![]() ),从而求A;(2)由图象变换得到g(x)=6sin(4x+
),从而求A;(2)由图象变换得到g(x)=6sin(4x+ ![]() ),从而求函数的值域.
),从而求函数的值域.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知点列An(an , bn)(n∈N*)均为函数y=ax(a>0,a≠1)的图象上,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意连续三项能构成三角形的三边,则a的取值范围为( )
A.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
C.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.

(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为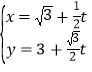 (t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2![]() cosθ.
cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程。
(2)求出直线l与曲线C相交后的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两曲线f(x)=cosx,g(x)= ![]() sinx,x∈(0,
sinx,x∈(0, ![]() )相交于点A.若两曲线在点A处的切线与x轴分别相交于B,C两点,则线段BC的长为 .
)相交于点A.若两曲线在点A处的切线与x轴分别相交于B,C两点,则线段BC的长为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为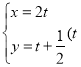 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学校本课程开设了A、B、C、D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(Ⅰ)求这3名学生选修课所有选法的总数;
(Ⅱ)求恰有2门选修课没有被这3名学生选择的概率;
(Ⅲ)求A选修课被这3名学生选择的人数![]() 的分布列 .
的分布列 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com